Radon (Rn-222) is an alpha-radioactive element in the decay chain of uranium. It is generated in the ground from the decay of radium and, as a gas, it occurs in high concentration in soil pore air. A number of physical factors and processes are involved in the generation and transfer of radon from mineral grains to soil gas and in the movements of radon-bearing soil air. The entry of soil gas into built spaces is controlled by the flow dynamics of soil air in the porous soil media and through a large variety of gaps, air-permeable building elements and openings in the structures in contact with soil or in floor structures in crawl space houses. Indoor radon concentrations vary widely depending on the uranium concentration of the terrain, soil permeability, entry from the ground to buildings and ventilation (1–3). Finland has one of the highest average residential radon-222 concentrations in the world, 96 Bq/m3, resulting in a mean annual effective dose of 1.6 mSv based on ICRP-65 from 1993 and a dose of 4.5 mSv based on the ICRP-137 (4–6). The new ICRP-137 from 2017 is based on both dosimetric estimates and epidemiology. The radiation dose is largely due to the short-lived progeny rather than radon itself. Dose to the bone marrow from inhaled radon progeny is substantially lower than that to the lung (7, 8).
Health effects of indoor radon
Uranium and hard-rock miners are exposed to very high concentrations of radon progeny and such occupational exposure has been shown to increase the risk of lung cancer (9). Lower residential radon concentrations have also been shown to increase the risk of lung cancer (10). The International Agency for Research on Cancer (IARC, World Health Organization) has classified radon as a recognized Group 1 human carcinogen (11). No excess of leukemia has been consistently associated with radon exposure in uranium miners (12–22).
Results from previous studies on the possible effect of exposure of indoor radon on risk of childhood leukemia have been largely negative but still inconclusive. The potential dose pathway for the association, in addition to the exposure of the red bone marrow, has been suggested to be through the exposure of lymphocytes within the tracheobronchial epithelium (23). Studies in Norway, France, the UK, and Switzerland showed no association, but a Danish case–control study with complete residential histories and a statistical model with 40% r2 reported an elevated risk (24–28). In these studies, exposure estimates were derived from model-based predictions of radon exposure (29–31). Efforts to construct a good prediction models have been made in the UK and detailed information on soil has been essential (32, 33). Some smaller studies have used actual radon measurements but shown no materially elevated risks (34–37). In addition, several ecological studies have evaluated the association between incidence rates and regional average radon levels and have consistently reported positive risk estimates (38).
Estimation of indoor radon
When estimating the effects of indoor radon, or most other environmental exposures, a direct measurement would be the optimal way to define exposure. However, that is not always possible due to practical reasons. To study risk factors of small expected effect size with sufficient statistical power, a large number of subjects is needed, and performing thousands or even millions of repeated on-site radon measurements does not currently appear feasible. Further, participation bias in measurement program is likely to be a significant problem. However, robust results have been reported using statistical models for predicting radon concentrations in similar scenarios (29–31). Many country-specific models have been published with varying performance (29, 39).
Low-rise residential buildings (single family houses, semi-detached houses and terraced houses) will be referred to as houses. Dwellings in multi-story block houses are called apartments.
Indoor radon concentrations are determined by a variety of factors in a complex chain of processes. In low-rise residential houses, the soil-borne radon gas dominates, with regard to indoor radon concentration. The main processes include concentration of uranium in mineral grain, emanation of radon from mineral grains to soil gas, movements of radon-bearing soil air in the porous soil media, and entry of radon-bearing soil gas into living spaces. In foundation structures, gaps, air-permeable building blocks, and openings in the structures increase the soil air entry into indoor spaces. The entry rate is controlled by the flow dynamics of soil air in the porous soil media and physical modelling shows that the air permeability of the sub-soil is a much more important factor than the effective area of the air leakage routes (40). Therefore, the highest values are measured in houses situated in hilly areas with porous soil of coarse gravel, for example on eskers (a long ridge of gravel or other sediment, typically having a winding course, deposited by meltwater from a retreating glacier or ice sheet). The lowest values in low-rise buildings are found in areas of impermeable clay. Air exchange in the building is the process of diluting radon concentration in indoor air (41).
In Finland, in apartment buildings soil-borne radon is not an important radon source, except for apartments on the lowest level and with floors in contact with soil. On upper floors, radon gas emanated from rock-based building materials, normally concrete elements, dominates. The national average indoor radon concentration caused by building materials in apartments is clearly lower (49 Bq/m3) than the average concentrations caused by soil-borne radon in low-rise residential houses (121 Bq/m3) (6). Also, the range of radon concentrations in apartments is narrower compared with houses as the percentage of measurements above 400 Bq/m3 in apartments was 0.7% in the national survey and 3.8% in houses. Uranium concentration of local gravel material can be utilized as a determinant for radon concentration in apartments because gravel has been used as concrete ballast material. Other important predictors of indoor radon are the dwellings age and the existence of cellars in detached houses (42, 43). Also, the story of the dwelling in blocks of flats has been shown to predict the concentration (44, 45). Seasonal variation has also been documented (43). Radon concentrations are highest during the heating season. Indoor radon measurements have been carried out in the period of November–April in Finland (46).
Modelling indoor radon concentrations has been proven to be particularly difficult as limited or no data are available on several important determinants. For example, the type of building foundation correlates strongly with radon concentrations but is rarely available (3, 43). The same stands true also for the type or source of gravel used for the foundation. However, due to the importance of the data from the original building soil, the effect of the lack in the knowledge of the transported layers of mineral material is decreased. Ventilation strategies, either natural or mechanical, are not included in the database of the Population Register Centre of Finland. However, history of the prevalence of ventilation strategies in Finnish low-rise residential buildings is well known based on national sample surveys (6, 41, 47). With regard to modelling, the effect of ventilation strategies seems to be limited compared with uranium concentration in soil or soil permeability (41).
The building code for radon prevention and the associated practical guidelines were revised in Finland in 2003–2004. Thereafter, preventive measures have become more common and effective and, in houses completed since 2006, indoor radon concentrations have been markedly reduced. These data are of great importance when constructing a statistical model. The national radon prevention study in 2009 showed that in houses with preventive measures, the radon concentration was on average reduced by ≥50% compared with houses with no preventive measures (47).
Furthermore, results from more than 200 000 individual radon measurements in Finnish dwellings are recorded in the database of the Radiation and Nuclear Safety Authority. In Finland, only regional indoor radon modelling has been conducted and no nationwide studies on modelling radon concentrations have been published.
Aims of the study
Using statistics, we modelled indoor radon concentration in a given dwelling using measurements from the nationwide database and internally validated its performance and robustness. Then we applied the model to examine potential association between residential radon and childhood leukemia using data from a nationwide childhood leukemia case–control study (48).
Methods
Radon measurements
We obtained results of all indoor radon measurements (N=244 059) from the database compiled by STUK – the Radiation and Nuclear Safety Authority and linked them to the building database of the Population Register Center by address and postal code. We used the oldest available measurement from each dwelling to minimize the effect of potential radon protection renovations. If there were two or more measurements with the same start dates, the one with higher measured concentration was used to maximize the models’ ability to recognize the high concentrations.
Combining databases
The Population Register Centers building database contains data on a dwelling type (house versus apartment), year of completion, floor area (m2), total area (m2), total volume (m3), number of floors, area of the basement, main building material (rock-based materials, wood, others) and air-conditioning. All predictive variables were required to be available from nationwide registries (Population Registry Center) and, thus, not all important predictors, that were available only in STUK’s radon database (type of foundation, radon protection, the floor of the dwelling), could be utilized in modelling.
The linkage of the measurements to the building database of the Population Register Center was based on street address and postal code as the key. This resulted in one-to-many linking problem due to multiple buildings in the same postal address. In such cases, we selected buildings with the best match in terms of building type, year of completion and coordinates.
To deal with the remaining discrepancies between databases (STUK’s and the Population Registry Center’s Building databases) after the primary selection, we created three sets of filtering criteria to acquire the best compromise between accuracy and sample size. We also aimed to explore whether there would be substantial differences in models with differently filtered radon datasets. The sample sizes of different filtering levels are represented in the figure 1. The first level required >100 m difference in Euclidean distance by coordinates, a >10-year difference in year of completion and no observable discrepancy in building type between the two databases. The second level required that there be no missing values in any of the filtering variables of the first level and thus all filters could be applied to every building (as the first level inhibited missing values from triggering the filter). The third level also allowed for no missing values and involved stricter criteria for >10 m Euclidean distance and identical year of completion. The numbers of buildings fulfilling the three sets of criteria are shown in the figure 1 (with other exclusions).
Figure 1
Flow chart of the indoor radon measurements and the necessary exclusions. To optimize both accuracy and sample size, we selected the first level of filtering as the basis for our main analyses.
a <100m difference in Euclidean distance by coordinates, <10-year difference in year of completion and no observable discrepancy in building type.
b <100m difference in Euclidean distance by coordinates, <10-year difference in year of completion and no observable discrepancy in building type and no missing values in any of the filtering variables.
c <10m difference in Euclidean distance by coordinates, a <10-year difference in year of completion and no observable discrepancy in building type and no missing values in any of the filtering variables.
Radon concentrations in houses and apartments were modelled separately as the major predictors differed based on the literature. Dwellings with missing or ambiguous building type were excluded. For the house model, the median postal-code-specific indoor radon concentration was derived from the 20% of the measurements sampled from the dataset left outside modelling to avoid using derivatives of the measurements as predictors. As the average number of dwellings per postal code area was relatively low and the total number of postal areas was relatively high, this resulted in some missing values (N=5697, 3.6%) and, also, some postal areas were represented by only few measurements. For the apartment model, we constructed a database of county-specific median radon concentrations in apartments based on two nationwide representative surveys (conducted in 1991 and 2006) (6, 49). The measurements from the 1991 survey were calibrated to match the values from the more recent survey.
Additional data for the models
To complement the model, we obtained data on the soil type as vector maps and terrain elevation as a 100 × 100 m square map from Geological Survey of Finland (GTK). Regarding the soil type, for each area, the map with the highest resolution (1:20 000, 1:50 000 and 1:100 000) available was used. STUK also provided us with an 8 × 8 km square map of soil uranium concentration (Bq/kg) (50). The vector maps for dwellings were evaluated using QGIS (v. 3.2.1) and square maps were evaluated with a basic R script.
Detailed soil types were classified into three categories by permeability. The classification was based on the grain size distribution of the soil type. Air permeability of soil types is closely related to grain size distribution. Soil air permeability is highest for coarse gravel (grain size 6–20 mm) and lowest for clay with a very low grain size (>0.002 mm). The database presents the soil type at the depth of 1 meter, which is representative of the depth of house foundations. Several terms were created to characterize year of construction: a categorical variable in 5-year intervals, as well as a separate indicator term for pre-1940 were used. For apartments, the latter term was defined with 1950 as the cut-off. The building material was classified as rock-based, wood, or other/unknown. We also created a binary variable to estimate exhaust fan-based ventilation: any type of ventilation based on the building registry and building completed before year 2000 for houses and any type of ventilation with building completed between 1950 and 2006 for apartments. The presence of a basement was modelled as a three-step variable (no basement, basement and dwelling built before 1990, basement and dwelling built after 1990) due to new prevalent practice of hill-side houses instead of full basement houses.
Modelling indoor radon
We applied multiple approaches for developing the two final radon prediction models. The methods were used similarly for both models from predictor selection to validation. First, we started with a log-linear model with all the available predictors. All continuous potential predictors were log-transformed. We used a backward selection algorithm starting with the full model and used multiple imputation to deal with the missing data. The proportions of missing data for each potential predictor are presented in the supplementary materialy (www.sjweh.fi/show_abstract.php?abstract_id=3867), table S1. We defined measured indoor radon outliers as values with z>3 and excluded them.
We then created two categorical models with radon concentrations divided into quartiles: a polynomial and a multinomial. We also tested a model with a binary dependent variable by dividing the radon concentration by its 80th percentile. Finally, we experimented with modern machine learning algorithms (random forest and deep neural networks) as an alternative to the traditional methods (51, 52). For random forest models, we set the number of trees grown to 2000 and 560 for apartments and houses, respectively, based on the point, where the model errors started to converge. Deep neural network was specified as a 4-layer network with 256, 128, 64, and 1 nodes with rectified linear unit as activation function in each except the output layer. The model was trained with 80% of the data with additional 20% used as validation for each epoch for 1000 epochs or until convergence according to mean squared error.
We used five-fold cross validation to explore the robustness and potential over-fitting of the log-linear model. We also calculated the Spearman correlation between the measured and predicted indoor radon concentrations. Categorical models were evaluated with Cohen’s kappa. We performed sensitivity analyses on different levels of filtering regarding the slight discrepancies between databases.
Childhood leukemia case–control study
The indoor radon exposure was predicted with log-linear model for the cases and controls using our nationwide case-control dataset (48). Briefly, the cases included all Finnish children diagnosed with childhood leukemia during 1990–2011. The 1100 cases were identified from Finnish Cancer Registry (M9800 - M9948 in ICD-O-3). Three controls were individually matched on sex and year of birth to each case from the Finnish Population Register Center. Each control was assigned a reference date to match the diagnosis of the respective case. We assumed a two-year latency based on results summarized by UNSCEAR, which automatically results in null exposure for subjects less than two years of age at their reference date as well as their controls (53). These cases and their respective controls were excluded from the analyses. We obtained also complete residential histories which yielded, in total, 7334 residencies with the aforementioned latency period. As a sensitivity analysis, we experimented with a five-year latency period.
The cases were classified by leukemia subtype into pre-B-ALL (precursor B-cell acute lymphoblastic leukemia), T-ALL (T-cell acute lympoblastic leukemia), unspecified ALL, AML (acute myeloid leukemia) and others. The genetic subtypes were obtained from the hospital records. We obtained data on gestational age, birth weight, maternal smoking from the Medical Birth Registry. Diagnoses of Down syndrome and other congenital malformations were obtained from the Congenital Malformation Registry. In addition, we obtained data on parental education, occupation, and socioeconomic status from Statistics Finland.
When applying the model to the childhood leukemia dataset for subjects (3.0% for cases and 2.6% for controls) with only municipality of residence available (for at least one residence), we used municipality-specific radon estimates. For residential periods abroad (1.4% for cases and 0.7% for controls), we used worldwide indoor radon average 39 Bq/m3 (54). In the rare cases where a dwelling could not be classified as either a house or an apartment, we also used the municipality-specific median (1.2% for cases and 1.2% for controls). Otherwise, we applied the model after using multiple imputation for missing data on variables required for the prediction. As the dependent variable of the model was log-transformed before fitting the curve, the predictions represent geometric means of the estimated indoor radon concentrations when transformed back into Bq/m3.
Radon exposure prediction
We calculated cumulative radon exposure as Bq/m3 integrating over time to cover the whole residential history taking two-year latency period into account and divided it into quartiles for the conditional logistic regression analyses. We also calculated the average concentration of the exposure period by dividing the cumulative exposure with the total length of the exposure period. Cumulative exposure accumulates with age and, thus, is highly correlated with it. The analyses were adjusted for potential confounders: Down syndrome (yes or no), large birth weight (LGA) (exceeds 90th birth weight percentile in relation to gestational duration), terrestrial gamma radiation and Chernobyl fallout [cumulative red bone marrow equivalent dose (mSv)], cumulative red bone marrow dose from CT exposure (mGy), maternal smoking during pregnancy (yes or no), as well as parental socioeconomic status and education. Both socioeconomic status and education were known individually for each parent. Socioeconomic status was classified into five classes (self-employed, upper level employee, lower level employee, manual worker and other) and education into three levels (upper secondary, bachelor’s degree, master’s or doctor’s degree) (55).
Statistical analysis
All analyses were performed using R software version 3.4.0. For the modelling and visualization, the R libraries included: multiple imputation (Amelia, v. 1.7.5), k-fold cross validation (DAAG, v. 1.22), Cohen’s kappa (psych, v. 1.8.4), Bland-Altman plot (BlandAltmanLeh, v. 0.3.1; ggExtra, v. 0.8; ggplot2, v. 3.1.0), ordered logistic regression (MASS, v. 7.3-51), Brant’s test (brant, v. 0.2-0) multinomial logistic regression (nnet, v. 7.3-12), random forests (randomForest, v. 4.6-14), keras (keras, v. 2.2.0). The risk analyses after prediction were carried out with conditional logistic regression from the library survival (v. 2.43-1). Variance inflation was examined using car-library (v. 3.0-2). We used 5% as the significance threshold and all reported p-values are two-sided. For multiple testing corrections we used the Benjamini-Hochberg method. Effect modification was investigated by including interaction terms into the model and evaluating improvement in model fit.
Results
Radon measurements
The median indoor radon concentration in 93 219 unique linked dwellings from the STUK database was 137.3 Bq/m3 (IQR 68.0 Bq/m3, 267.4 Bq/m3), with the 95th percentile 732.7 Bq/m3, the 99th percentile 1913.0 Bq/m3 and the maximum 38,883 Bq/m3. The distribution was log-normal and after log-transformation, the distribution was normalized when evaluated using a Q-Q plot.
After exclusions, the material included 73 903 (94.1%) houses and 3709 (4.7%) apartments, with median radon concentrations 143 Bq/m3 (IQR 71 Bq/m3, 276 Bq/m3) and 66 Bq/m3 (IQR 38 Bq/m3, 134 Bq/m3), respectively. The descriptive statistics and distributions of predictors are represented in tables 1a and b by indoor radon quartiles.
Table 1a
Proportions and statistics of the predictors by measured indoor radon quartiles. [IQR=interquartile range.]
| 1st quartile | 2nd quartile | 3rd quartile | 4th quartile | |||||
|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|||||
| Houses N=14 770 (43.3 Bq/m3) a | Apartments N=932 (27.0 Bq/m3) a | Houses N=14 767 (103 Bq/m3) a | Apartments N=917 (50.6 Bq/m3) a | Houses N=14 768 (196 Bq/m3) a | Apartments N=924 (88.0 Bq/m3) a | Houses N=14 768 (438 Bq/m3) a | Apartments N=925 (250 Bq/m3) a | |
|
|
|
|
|
|
|
|
|
|
| N (%) | N (%) | N (%) | N (%) | N (%) | N (%) | N (%) | N (%) | |
| Building material | ||||||||
| Rock-based | 1712 (11.6%) | 883 (94.6%) | 2211 (15.0%) | 867 (94.5%) | 2445 (16.6%) | 877 (94.9%) | 2602 (17.6%) | 805 (87.0%) |
| Wood | 12802 (86.7%) | 44 (4.7%) | 12286 (83.2%) | 38 (4.1%) | 12087 (81.8%) | 36 (3.9%) | 11973 (81.1%) | 109 (11.8%) |
| Other | 256 (1.7%) | 6 (0.6%) | 270 (1.8%) | 12 (1.3%) | 236 (1.6%) | 11 (1.2%) | 193 (1.3%) | 11 (1.2%) |
| Soil permeability | ||||||||
| Impermeable | 6166 (41.8%) | 275 (29.5%) | 6124 (41.5%) | 273 (29.8%) | 6094 (41.3%) | 301 (34.7%) | 5246 (35.5%) | 253 (27.4%) |
| Moderately permeable | 6029 (40.8%) | 186 (19.9%) | 5989 (40.6%) | 150 (16.4%) | 5775 (39.1%) | 175 (18.9%) | 5230 (35.4%) | 163 (17.7%) |
| Highly permeable | 1910 (12.9%) | 97 (10.4%) | 2097 (14.2%) | 120 (13.1%) | 2489 (16.9%) | 127 (13.7%) | 3996 (27.1%) | 290 (31.4%) |
| Formation by ice-age | ||||||||
| On a formation | 1341 (9.1%) | 82 (8.8%) | 1630 (11.0%) | 99 (10.8%) | 1999 (13.5%) | 108 (11.7%) | 3365 (22.8%) | 257 (27.8%) |
| Mechanical ventilation | ||||||||
| Exhaust ventilation (approx.) b | 1723 (11.7%) | 459 (49.2%) | 2701 (18.3%) | 457 (49.8%) | 3425 (23.2%) | 476 (51.5%) | 3622 (24.5%) | 506 (54.7%) |
| Basement | ||||||||
| Yes (built before 1990) | 404 (2.7%) | 85 (9.1%) | 433 (2.9%) | 52 (5.7%) | 468 (3.2%) | 35 (3.8%) | 479 (3.2%) | 46 (5.0%) |
| Yes (built after 1990) | 429 (2.9%) | 57 (6.1%) | 336 (2.3%) | 50 (5.5%) | 286 (1.9%) | 49 (5.3%) | 286 (1.9%) | 58 (6.3%) |
|
|
||||||||
| Number of floors | ||||||||
| Median | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 3 |
| IQR | 1–2 | 3–6 | 1–2 | 3–4 | 1–2 | 4–5 | 1–2 | 2–4 |
| p95 | 2 | 8 | 2 | 8 | 2 | 8 | 2 | 7 |
Table 1b
Proportions and statistics of the predictors by measured indoor radon quartiles. [IQR=interquartile range.]
| I quartile | II quartile | III quartile | IV quartile | |||||
|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|||||
| Houses (10.3–95.0) a | Apartments (15.3–85.7) a | Houses (10.3–95.0) a | Apartments (11.0–85.8) a | Houses (10.7–95.0) b | Apartments (13.9–83.4) b | Houses (10.7–95.0) b | Apartments (13.9–87.1) b | |
|
|
|
|
|
|
|
|
|
|
| Median (IQR) | Median (IQR) | Median (IQR) | Median (IQR) | Median (IQR) | Median (IQR) | Median (IQR) | Median (IQR) | |
| Number of floors | 1 (1–2) | 4 (3–6) | 1 (1–2) | 4 (3–4) | 1 (1–2) | 4 (4–5) | 1 (1–2) | 3 (2–4) |
| Soil’s uranium (Bq/kg) | 39.4 (29.6–51.6) | 45.2 (31.5–62.5) | 43.7 (32.3–53.7) | 51.8 (34.5–66.3) | 46.3 (36.9–56.6) | 51.8 (41.4–66.3) | 48.7 (40.2–58.1) | 51.8 (45.0–59.7) |
| Area of the floors (m2) | 154 (116–200) | 1973 (1322–3101) | 160 (120–205) | 2016 (1298–2928) | 163 (126–206) | 1784 (1187–2725) | 160 (127–202) | 1365 (751–2050) |
| Total area (m2) | 184 (145–235) | 2420 (1580–3724) | 184 (149–244) | 2396 (1538–3610) | 184 (151–245) | 2088 (1284–3320) | 184 (151244) | 1552 (822–2336) |
| Total volume (m3) | 565 (455–750) | 7382 (4941–11597) | 570 (455–766) | 7280 (4840–10738) | 566 (459–766) | 6482 (4250–9971) | 560 (454–750) | 4895 (2780–7340) |
| Year of completion (year) | 1979 (1956–2004) | 1973 (1963–1986) | 1981 (1963–1995) | 1972 (1964–1984) | 1983 (1970–1992) | 1974 (1965–1985) | 1983 (1973–1991) | 1979 (1968–1988) |
| Terrain elevation (m) | 84 (31–106) | 36 (13–101) | 87 (43–108) | 38 (17–96) | 89 (46–109) | 49 (17–101) | 91 (50–112) | 83 (25–114) |
| Radon (area b-log) | 6.67 (6.10–7.07) | 3.67 (3.49–3.71) | 6.63 (6.11–6.97) | 3.72 (3.61–3.73) | 6.68 (6.31–6.95) | 3.78 (3.71–3.92) | 6.82 (6.56–7.01) | 3.85 (3.71–4.08) |
Modelling indoor radon concentrations
The final predictors, their estimates and confidence intervals (CI) with adjusted P-values for the log-linear model are reported in tables 2a, b and c. For the house model, most of the selected predictors had a highly statistically significant effect due to large sample size. Especially for the houses, the construction year displayed an inverted U-shaped curve relationship with indoor radon, with lower concentrations in newer buildings due to stricter radon protection regulation. Rock-based building materials were associated with higher residential radon than wood as a building material, and higher indoor radon concentrations were also associated with more porous soil. Uranium concentration in soil exerted a major influence in the house model. In general, we identified fewer predictors with mostly smaller coefficients for apartments.
Table 2a
Coefficients and 95% confidence intervals (CI) of the predictors from the final model after backwards selection algorithm.
| Predictor | Apartments | Houses | ||
|---|---|---|---|---|
|
|
|
|||
| coefficent (95% CI) | P-value a | coefficent (95% CI) | P-value a | |
| Other materials (ref) b | 0 | |||
| Mainly built from rock-based materials | - | - | 0.08 (0.02–0.14) | 0.01 |
| Mainly built from wood | - | - | -0.07 (-0.13–0.01) | 0.02 |
| Unknown or other soil (ref) b | 0 | 0 | ||
| Impermeable soil | 0.04 (-0.02–0.12) | 0.4 | 0.10 (0.06–0.14) | <0.001 |
| Moderate permeability soil | 0.08 (-0.01–0.18) | 0.10 | 0.16 (0.12–0.21) | <0.001 |
| Highly permeable soil | 0.31 (0.13–0.48) | 0.001 | 0.27 (0.22–0.32) | <0.001 |
| Not on a land formation by the ice-age (ref) b | 0 | 0 | ||
| On a land formation by the ice-age | 0.23 (0.06–0.41) | 0.02 | 0.27 (0.24–0.3) | <0.001 |
| No basement (ref) b | 0 | |||
| Basement, dwelling built before 1990 | - | - | 0.33 (0.28–0.37) | <0.001 |
| Basement, dwelling built after 1990 | - | - | 0.09 (0.04–0.14) | 0.001 |
Table 2b
Coefficients and 95% confidence intervals (CI) of the predictors from the final model after backwards selection algorithm.
| Predictor | Apartments | Houses | ||
|---|---|---|---|---|
|
|
|
|||
| coefficent (95% CI) | P-value a | coefficent (95% CI) | P-value a | |
| Before the first category (ref) b | 0 | 0 | ||
| Built in | ||||
| 1940–1945 | - | - | 0.11 (0.04–0.19) | 0.005 |
| 1945–1950 | - | - | 0.01 (-0.04–0.05) | 0.8 |
| 1950–1955 | -0.33 (-0.52– -0.13) | 0.002 | -0.14 (-0.19– -0.1) | <0.001 |
| 1955–1960 | -0.25 (-0.42– -0.09) | 0.006 | -0.20 (-0.25– -0.16) | <0.001 |
| 1960–1965 | -0.32 (-0.46– -0.18) | <0.001 | 0.10 (0.05–0.15) | <0.001 |
| 1965–1970 | -0.25 (-0.38– -0.12) | 0.001 | 0.22 (0.18–0.27) | <0.001 |
| 1970–1975 | -0.13 (-0.25– -0.01) | 0.06 | 0.35 (0.31–0.39) | <0.001 |
| 1975–1980 | 0.01 (-0.13–0.15) | 0.90 | 0.43 (0.39–0.47) | <0.001 |
| 1980–1985 | 0.26 (0.12–0.39) | 0.001 | 0.61 (0.57–0.65) | <0.001 |
| 1985–1990 | 0.22 (0.08–0.36) | 0.005 | 0.57 (0.53–0.61) | <0.001 |
| 1990–1995 | 0.14 (-0.02–0.31) | 0.10 | 0.50 (0.45–0.55) | <0.001 |
| 1995–2000 | -0.04 (-0.23–0.15) | 0.70 | 0.32 (0.27–0.37) | <0.001 |
| 2000–2005 | -0.06 (-0.27–0.14) | 0.60 | 0.08 (0.04–0.13) | <0.001 |
| 2005–2010 | -0.43 (-0.66– -0.2) | 0.001 | -0.14 (-0.19– -0.1) | <0.001 |
| 2010–2015 | -0.45 (-0.72– -0.18) | 0.003 | -0.53 (-0.57– -0.48) | <0.001 |
| 2015–2020 | 0.06 (-0.86–0.98) | 0.90 | -0.76 (-0.9– -0.61) | <0.001 |
Table 2c
Coefficients and 95% confidence intervals (CI) of the predictors from the final model after backwards selection algorithm.
| Predictor | Apartments | Houses | ||
|---|---|---|---|---|
|
|
|
|||
| coefficent (95% CI) | P-value a | coefficent (95% CI) | P-value a | |
| Number of floors | -0.16 (-0.25– -0.07) | 0.001 | -0.15 (-0.18– -0.13) | <0.001 |
| Floor area | -0.13 (-0.07– -0.19) | <0.001 | -0.05 (-0.07– -0.03) | <0.001 |
| Total area of the building | - | - | - | - |
| Total volume of the building | - | - | -0.01 (-0.03–0.00) | 0.2 |
| Elevation from sea level | 0.07 (0.03–0.10) | 0.001 | 0.15 (0.14–0.16) | <0.001 |
| Soil’s uranium concentration | 0.17 (0.06–0.29) | 0.007 | 0.70 (0.68–0.73) | <0.001 |
| County specific median radon | 0.96 (0.79–1.13) | <0.001 | - | - |
| Postal area specific median radon | - | - | 0.09 (0.08–0.10) | <0.001 |
| Intercept | 0.77 (0.19–1.35) | 0.02 | 1.09 (0.92–1.25) | <0.001 |
For both models (houses and apartments), the year of completion was an important predictor. It explained 10.6% and 4.61% of the variance and for the house and apartments, respectively. Soil permeability was also influential (houses 2.97% and apartments 7.05%). The other proportions of the variation explained by each predictor are reported in table 3. For the final log-linear house model, we observed Akaike’s information criterion (AIC) 157 739 and Bayesian information criterion (BIC) 158 036 and for the apartment model AIC 9993 and BIC 10 161.
Table 3
The proportions of explained variance by predictor
| Predictor | Variance explained (%) | |
|---|---|---|
|
|
||
| Apartments | House | |
| Soil permeability | 7.05 | 2.96 |
| County specific median radon concentration a | 6.50 | - |
| Year of completion (5-year intervals) | 4.91 | 10.5 |
| Number of floors | 1.27 | 0.17 |
| Floor area | 0.46 | 0.11 |
| Formation by the ice-age (eskers etc.) | 0.26 | 0.51 |
| Elevation | 0.19 | 1.46 |
| Uranium concentration of the soil | 0.003 | 3.57 |
| Building material | - | 0.48 |
| Basement b | - | 0.07 |
| Total volume of the building | - | 0.03 |
| Indoor radon median in the postal area c | - | 0.88 |
| Residuals | 79.4 | 79.3 |
Performance of the models
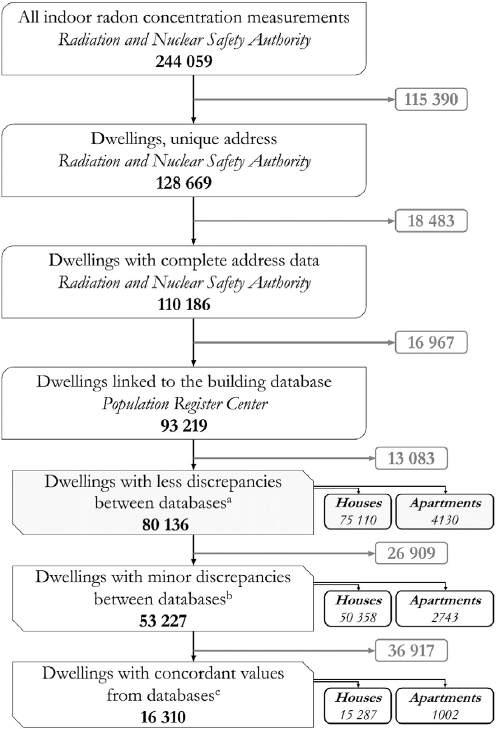
The final model of the log-transformed indoor radon concentration reached r2 of 0.21 for the house model and 0.20 the apartment model. The Spearman correlation between the measured and predicted values in the validation dataset was 0.45 for the houses and 0.44 for the apartments. The scatterplots of measured and predicted indoor radon concentrations also showed only a modest correlation with a narrower range of predicted than observed concentrations (figure 2), but both models were unable to accurately identify the lowest and highest radon concentrations (figure 3). In the five-fold cross-validation with 80–20 split, the models appeared robust with no indication of substantial over-fitting for either model. The mean squared error was 0.84 for the houses and 0.88 for the apartments. We observed variance inflation due to multicollinearity of the predictors. For the apartments, the predictors with generalized variance-inflation (GVIF) >2 were soil permeability (5.1), formation by ice-age (4.3), year of completion (2.3) and soil uranium concentration (2.3). For the house model, five predictors showed GVIF >2: soil permeability (2.6), formation by ice-age (2.4), year of completion (2.6), floor area (2.3) and total volume (2.2).
Figure 2
Scatter-plot of the measured and predicted indoor radon concentrations. Black dots represent measurement prediction pairs from houses and the grey ones are for apartments.
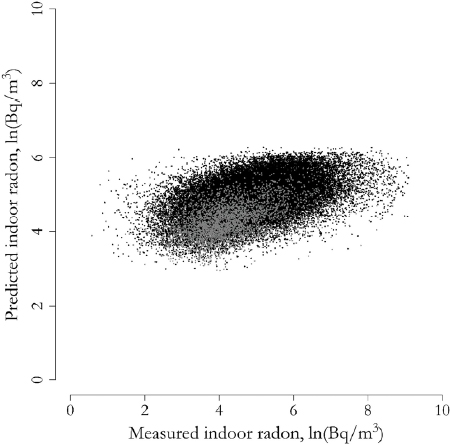
Figure 3
Bland-Altman plot of the predicted and measured indoor radon concentrations. The results from the house model are on the left with black dots. The apartment model is represented on the right side with grey dots. X axes represent the mean of the predicted and measured indoor radon concentration and on the Y axes is the difference (measured – predicted) of the values.
The weighted Cohen’s kappa for measured and predicted values by quartiles of measured indoor radon was 0.33 for houses and 0.38 for apartments. If only one split at 80th percentile was used, the weighted kappa was 0.10 for houses and 0.25 for apartments.
Exploratory modelling attempts
In exploratory analyses, the predictors of both dwelling types remained largely similar when an ordered logistic regression was used instead of the log-linear model to predict indoor radon in quartiles, but the assumption of parallel lines was not met for the categorized year of completion when evaluated with Brant’s test. This also applied to multinomial logistic regression. Ordinary logistic regression for binary radon split at p80 gave poor results.
We did not observe major changes in r2 (0.21–0.24 for houses and 0.20–0.24 for apartments) or in the coefficients when different levels of measurement filtering were used. Using modern machine learning methods, we were able to markedly improve the coefficient of determination [random forest (apartments 0.23, houses 0.28), deep neural network (apartments 0.19, houses 0.18)]. We also observed lower coefficients of determination when using the newest available radon concentration for each dwelling.
Childhood leukemia case-control data
After exclusions, we included 1093 (4 had prohibition of data use and 3 had incorrect identification codes) childhood leukemia cases diagnosed in 1990–2011. Of these, 826 (75.6%) were pre-B-ALL, 64 (5.9%) were T-ALL, 20 were unclassified ALL (1.8%), 146 were AML (13.6%), and 34 were other (3.1%). A majority of the cases were diagnosed at age 2–7 years, and the median age was 4.52 [interquartile range (IQR) 2.72, 8.23]. Down syndrome, intrauterine growth, and maternal smoking during pregnancy were associated with risk of childhood leukemia (table S2).
In total, there were 7443 different dwellings (1839 for cases and 5604 for controls) in the subjects’ residential histories using the two-year latency period. The residential radon concentrations were estimated with either the house (56.1%, N=1032 for cases and 54.9%, N=3079 for controls) or the apartment model (38.3%, N=704 for cases and 40.5%, N=2271 for controls), except for 5.6% for cases and 4.5% for controls for whom municipality-specific medians were imputed due to lack of dwelling data.
Evaluating the model against direct measurements
Direct measurements were available for 1.4% (N=103) of the subjects’ residential periods (1.4%, N=25 for cases and 1.4%, N=78 for controls) when linking by address, city and the time period of the measurement to STUK radon database. The Spearman correlation between the predicted and measured radon concentrations of the subjects was 0.36 and r2 was 0.10 after log-transformation. If direct measurements were matched also by year of completion (maximum 1-year discrepancy) and by coordinates (maximum 100 m Euclidean distance), there were, in total, 55 measurements [14 (25%) for cases, and 41 (75%) for controls], and the Spearman correlation rose to 0.45 and the r2 became 0.11.
Predicted radon concentrations
We made predictions of indoor radon concentration for each residential period with both the log-linear and random forest models. The correlation between these predictions for apartments was 0.52 and 0.49 for houses. Respectively, the correlation between the cumulative exposures (Bq/m3 years) of subjects was higher (0.93) and for the average concentration it was only 0.29, reflecting the effect of the total duration of all residential periods of each subject.
Using the log-linear model, the median predicted cumulative indoor radon exposure was 301 Bq/m3 years (IQR 121 Bq/m3 years, 625 Bq/m3 years) for the cases and 292 Bq/m3 years (IQR 116 Bq/m3 years, 636 Bq/m3 years) for the controls. The median of the time-weighted average indoor radon concentration was 92 Bq/m3 (IQR 68 Bq/m3, 123 Bq/m3) for cases and 89 Bq/m3 (IQR 67 Bq/m3, 121 Bq/m3) for controls. For the random forests model, the median cumulative exposure among the cases was 357 Bq/m3 years (IQR 151 Bq/m3 years, 789 Bq/m3 years) and for the controls 357 Bq/m3 years (IQR 152 Bq/m3 years, 799 Bq/m3 years). The median of the average concentration for cases was 107 Bq/m3 (IQR 93 Bq/m3, 127 Bq/m3) and for controls 107 Bq/m3 (IQR 93 Bq/m3, 128 Bq/m3).
Risk analyses
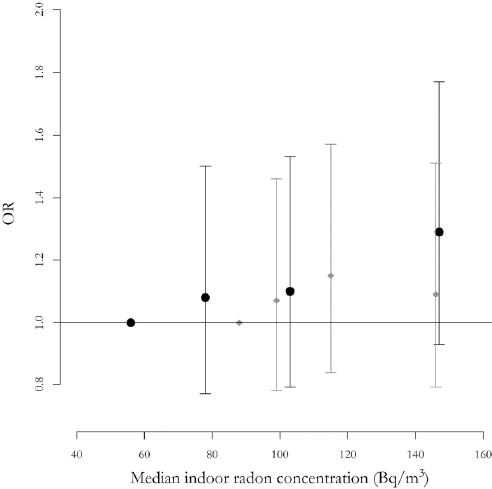
In unadjusted analysis of exposure predicted with the log-linear models, we observed an odds ratio (OR) of 0.87 (95% CI 0.63–1.19) for an increase of 1000 Bq/m3 years in cumulative radon exposure. When the model was adjusted for potential confounders the OR was 1.06 (95% CI 0.59–1.92). The results from both unadjusted and adjusted models for cumulative exposure, average concentration and quartiles are presented in table 4 based on log-linear and random forest predictions. The dose–response curves based on quartiles are presented in figure 4 for predictions from both modelling approaches.
Table 4
Odds ratios (OR) and their confidence intervals (CI) from conditional logistic regression analyses about the effect of predicted indoor radon concentration on childhood leukemia. Only subjects with non-zero exposure were included. A latency period of two years was used. [Ref=rerence classes for factors.]
Figure 4
Dose–response curve by quartiles of estimated indoor radon exposure based on predictions from the log-linear and random forest models. The point estimates and their confidence intervals (CI) were calculated with conditional logistic regression using a latency period of two years. The location of the point estimates and their respective CI on the X-axis is determined by the median of predicted indoor radon exposure inside each group. Grey color with diamond shapes is used to represent results from the random forest models and the black dots represent estimates from the log-linear models.
Exploratory and sensitivity analyses
In exploratory subgroup analyses for ALL patients with the log-linear model, we found an adjusted OR of 1.32 (95% CI 0.67–2.60) for every 1000 Bq/m3-years. Similarly, for subjects diagnosed before turning 6 years, the OR was 3.53 (95% CI 0.80–15.5). All subgroup analyses for both cumulative exposure and average concentration with log-linear and random forest predictions are shown in the supplementary table S3. The interaction term was not significant for subtypes nor age-groups.
As sensitivity analysis, we explored the effect of a longer, 5-year, latency period (489 cases and 1467 controls). In unadjusted analyses with log-linear model, we observed an OR of 0.70 (95% CI 0.42–1.18) for an increase of 1000 Bq/m3 in cumulative exposure and when adjusted the similar OR was 0.93 (95% CI 0.33–2.63). The analysis of quartiles of average concentration showed no evidence of elevated risk and the central estimates of all but the reference quartile were below unity (data not shown).
Discussion
Main findings
We constructed two prediction models to estimate indoor radon concentrations in Finland using both technical properties of the buildings and geological properties of the terrain under the building. Our models performed reasonably well compared to previous modelling attempts, showed no imminent signs of overfitting and behaved robustly in multiple sensitivity analyses. However, the prediction model was unable to distinguish radon concentration deviating strongly from the average but modelling the highest concentrations (>10 000 Bq/m3) was never the aim as they are not reachable with traditionally available data. We applied the model to a nationwide register-based case-control dataset of childhood leukemia and observed a slight, non-significant trend risk, with the OR 1.1–1.3 (95% CI 0.79–1.77) for radon concentrations >120 Bq/m3.
The distributions of the predictions produced by our models (92 Bq/m3 for cases, 89 Bq/m3 for controls) were in line with the previously published median Finnish indoor radon concentration (96 Bq/m3) (6, 56). The performance of our main model was similar (r2 = 0.21) to the recent, similarly constructed model from Switzerland (29). Higher coefficients of determination in some previous country-specific models may be related to smaller numbers of measurements (30, 57, 58). We were also able to reach slightly higher coefficients of determination using the random forest machine learning method. However, the small absolute difference in r2 (maximum 0.07 units), suggests no dramatic improvement over the simpler, and thus to some degree more preferable, classic approach with the log-linear model.
Strengths of the study
Regardless of the sub-optimal performance, the various strengths of our study, with its sophisticated modern machine-learning methods, make it the most up-to-date statistics-based attempt to study indoor radon and childhood leukemia. Our prediction models were created with a comprehensive roster of predictors. Both building properties and geological variables were used. The predictors were collected from nationwide registries. The sample size of direct indoor radon measurements, on which the model is based, is the largest to date. We used multiple approaches when building the optimal model and also saw potential in modern machine-learning methods, especially in the random forest method.
Limitations of the study
However, our study had also limitations. First, our prediction model failed to identify residences toward the high and low ends of the indoor radon range, as is apparent in the Bland-Altman plots. This shortcoming was not rectified by the machine learning methods. Unlike most countries, Finnish indoor radon concentrations can be >10 000 Bq/m3, which poses major challenges for the prediction and also means that models created for other European countries cannot be applied to the Finnish predictions. To combat the issue, we used the oldest measurements when there were multiple available to avoid the interference of potential radon protection installations and also used the highest available measurement from each measurement session if concentrations were, for example, measured in multiple rooms. This approach resulted in higher coefficients of determination. In the Swiss study using an approach comparable to our log-linear model, the median predicted radon concentration was 77.7 Bq/m3 and the 90th percentile was 139.9 Bq/m3 (29). The respective statistics in our data were 89.9 Bq/m3 and 154.1 Bq/m3. In the Danish study, the median of the predicted concentrations was considerably lower (41 Bq/m3) (26).
Second, even though the used soil type maps were vector-based with resolution sufficient to minimize misclassification, the soil types in maps were defined manually and borders between soil types may involve some inaccuracies.
Third, multicollinearity of the predictors cannot be entirely avoided and this may weaken the distinction between predictor contributions and this was observed as higher variation inflation factors. The year of completion reflects multiple building properties and it was one of the strongest predictors of indoor radon also included in the model. It is, however, a proxy indicator for building techniques that we were unable to capture directly and is therefore a suboptimal predictor. The missing important predictors included the type of foundation and the type of stabilizing soil used directly under the foundation as well as accurate ventilation flow patterns.
Fourth, the county-specific median indoor radon concentrations in the apartment model are based on measurements that are included in the apartment model, introducing an element of circular logic. Excluding the survey measurements would have decreased the apartment sample roughly by half. This issue was avoided with houses by randomly selecting a 20% subsample, which was then left outside modelling. Overall, these issues likely overestimated the predictive capacity of our models.
Finally, when the performance of the model was evaluated with direct measurements, we saw some signs of overfitting as the correlation coefficients and the r2 values were lower than in other means of estimating model performance. Using more stringent criteria for identifying direct measurements did not completely solve the issue. Also, the predictions made by log-linear and random forest models were not highly similar which also displays another uncertainty in our exposure assessment strategy.
The performance of the prediction model was not optimal despite large and high-quality data available for the predictors. The fact that even rich data combined with sophisticated statistical methods fails to capture variability in indoor radon between dwellings shows that results obtained in some other countries are not applicable in the Finnish context and casts some doubt about their broader generalizability. Differences may also reflect a more complex set of determinants in the Finnish context (and broader range of radon levels). Improved prediction models would likely require new modelling approaches or more complete building characteristics.
Integration of the findings with previous studies
As in the recent Norwegian and Swiss analyses, we did not observe a significantly increased risk of childhood leukemia associated with indoor radon. Hauri et al (26) compared the highest 90th percentile to subjects below median and reported an adjusted HR of 0.95 (95% CI 0.63–1.43). Kollerud et al (31) found an adjusted HR of 0.93 (95% CI 0.76, 1.13) per 100 Bq/m3 increment. Also, the analyses from United-Kingdom and France did not report increased risks related to higher indoor radon concentrations (27, 28). The British study reported an RR of 1.03 (95% CI 0.96–1.11) for every 1 mSv increase in cumulative red bone marrow dose as the French study reported and standardized incidence ratio of 1.01 (95% CI 0.91–1.12) for an increase of 100 Bq/m3 in the indoor radon concentration.
Interestingly, a Danish study by Raaschou-Nielsen et al (24) reported an increased risk for childhood ALL (RR 1.53, 95% CI 1.05–2.30 for a 1000 Bq/m3-year increase in cumulative exposure). The Danish study was based on a radon prediction model with a high r2 (40%). They were also able to utilize complete residential histories and adjust for a number of potential confounders. The CI of the Danish study overlap with the results we observed.
Several small case–control studies have used direct residential radon measurements and failed to show a consistent exposure–effect gradient (34–37). They have been frequently limited, however, by lack of complete residential histories and potential selection bias.
When applying the model to our childhood leukemia case–control dataset, we were able to use complete residential histories. The register-based approach minimized selection bias. We adjusted for multiple potential confounders and used a two-year latency period to focus on etiologically relevant exposure.
However, the conclusions that can be drawn from the risk analyses are dependent on our ability to predict the exposure, and the limitations in the prediction model performance are likely to introduce exposure misclassification. As this is most likely similar for cases and controls, non-differential random error is expected to dilute any true effect and a null result may reflect either real lack of an effect or an effect largely masked by misclassification. Also, the dilemma of optimal research strategy remains in choosing between an analysis with inaccurate exposure assessment in a large and representative sample (as register-based studies with predicted radon) or an analysis with accurate direct measurements in a smaller sample potentially affected by selection bias.
Concluding remarks
Our modelling of indoor radon concentration involves major uncertainties, and the results should be interpreted with caution. However, we observed a slight non-significant risk of childhood leukemia related to higher average indoor radon concentrations and results are suggestive of a higher risk for ALL patients and patients under six years of age. In future studies using predictive models, identifying the dwellings with the high radon concentrations, preferably up to 2000 Bq/m3, should be prioritized and, whenever possible, direct measurements should be chosen over modelling.



