Though typically not the most common musculoskeletal disorder (MSD) reported in industry, carpal tunnel syndrome (CTS) has a harmful effect on both workers and employers. In 2012, the most recent reporting year, the US Bureau of Labor Statistics (BLS) reported that CTS resulted in a median of 30 lost workdays per case, more than 2.5 times the median of 12 lost days per case for musculoskeletal injuries in general (1). The average cost of a CTS workers’ compensation claim has been reported as USD 20 405 (2). Further, workers who are diagnosed with CTS suffer substantial loss of wages and can become chronically debilitated, both in the workplace and their daily lives (3). Thus, information, tools and strategies for the prevention of CTS in industry deserve continued attention.
Several non-occupational risk factors have shown association with CTS, including: age, female gender, obesity, pregnancy, and comorbid diseases such as diabetes mellitus, rheumatoid arthritis, and thyroid disease (4–12). More recently, psychosocial factors such as job strain, lack of coworker support, and low decision latitude have received some attention and have showed mixed associations with CTS (13–17). The challenge for employers is that non-occupational risk factors are often difficult or impossible to modify. Psychosocial risk factors, while presumably modifiable, remain under-studied and thus it is unclear how to allocate resources to mitigate risks from such factors.
The relationships between job physical exposures and CTS have received considerable attention and associations between CTS and exposure to high force of exertion, high repetition of exertions, deviated wrist postures, and hand/arm vibration have been shown, (13, 18–23) though mostly through cross-sectional studies and/or using arbitrary measures of physical exposure (24). There is some evidence to suggest that physical exposure risk factors interact with one another (18–20, 25) and thus, from an industrial injury prevention perspective, perhaps the most valuable research is that which reports exposure–response relationships for models that include combinations of two or more physical exposure variables.
The American Conference of Governmental Industrial Hygienists’ (ACGIH) threshold limit value (TLV) for hand-activity level (HAL) (26) is among the most widely studied distal upper-limb physical exposure models for predicting risk of musculoskeletal injury. The TLV for HAL model includes two variables: (i) peak force (PF) and (ii) HAL, which conflates frequency of exertion and duty cycle of exertion into a single measure of repetition (27). The model compares PF and HAL levels for a task either graphically or computationally using the equation: score=PF/(10-HAL). According to the ACGIH, a score of <0.56 is said to be below the action limit (AL) and thus low risk. A score of >0.78 is said to be above the TLV and thus high risk, indicating that the task should be redesigned. Scores between the AL and the TLV are moderate risk and should receive additional surveillance and/or administrative controls if not redesign efforts (28).
Several prior studies have reported an association between the TLV for HAL model and CTS; however, most of these studies were either cross-sectional, or had limited sample size (16, 23, 25, 29–31). Recently, Bonfiglioli et al (32) conducted a prospective cohort study of >4000 production workers and clerks in Italy and reported a statistically significant association between the TLV for HAL model and CTS, with a monotonic increase in risk as exposure increased from below the AL to above the TLV. Bonfiglioli et al also studied PF and HAL as independent variables in a single multivariate model and their findings suggested that, while both PF and HAL were associated with incidence of CTS, HAL was the stronger of the two factors. They concluded that: (i) the current AL and TLV limits “might not be sufficiently protective for some workers”, and (ii) the “different strength of association of HAL and PF with CTS … deserves further investigation” (32).
This paper aims to compare the exposure–response relationships for: (i) PF, (ii) HAL, and (iii) the ACGIH TLV for HAL model (both as a continuous measure and using the ACGIH pre-defined AL and TLV) and incident CTS among a large sample of United States (US) workers.
Methods
The University of California, San Francisco Institutional Review Board, approved this study. All participating workers provided written informed consent.
The analyses presented in this paper were performed as part of a collaborative research project incorporating data from six independently conducted, National Institute for Occupational Safety and Health (NIOSH) sponsored, prospective cohort studies of risk factors for upper-extremity MSD conducted between 2001–2010 in the US. Raw data were combined from 4123 full-time male and female study participants aged ≥18 and employed by 54 predominantly manufacturing and service companies located in ten US states. The study cohort and data collection methods have been previously described in detail (24, 33). The following is a brief summary of those methods.
Physical exposure data collection
Blinded to worker health status, trained analysts quantified exposure to physical risk factors at baseline and during follow-up. The interval between initial and subsequent follow-up assessment of exposure to physical risk factors varied by site from weekly to annually (24). Workers who experienced changes in physical exposure during the follow-up period (eg, underwent a job change) had their physical exposures remeasured. Of interest for the current analyses were: (i) PF, as defined by the ACGIH (26) and measured using the Borg category ratio 0–10 (CR-10) rating scale (34), and (ii) HAL measured using Latko et al’s 0–10 verbal anchor scale (27). Both dominant hand PF and HAL were rated by trained analysts, either by direct observation in the field or from video analysis of worker tasks, and were estimated for each worker (24).
For workers performing multiple tasks during their work shift, both PF and HAL were measured for each task performed and time-weighted-averaging (TWA) was used to create single PF and HAL measures for each worker at given time-points. TWA PF and TWA HAL were further used to calculate the TLV for HAL score using the equation score=PF/(10-HAL). Subsequently, these scores were used to categorize the TLV for HAL into three groups using the ACGIH suggested limits: (i) below AL (score <0.56), (ii) between AL and TLV, and (iii) above TLV (score >0.78).
Demographic, symptom, and electrodiagnostic data collection
Age, gender, body mass index (BMI), and presence of comorbid diseases and conditions associated with CTS (ie, diabetes mellitus, rheumatoid arthritis, and thyroid disease) were collected at baseline. Hand symptoms were collected at baseline and at regular intervals ranging from weekly to annually during follow-up (33). Electrodiagnostic studies (EDS) of median nerve conduction velocity were performed at baseline and either annually or in response to CTS symptoms during follow-up (33). Analysts responsible for collection of demographic and health outcomes information were blinded to the workers’ physical exposures.
Case definition for CTS
The CTS case definition included symptoms plus abnormal EDS. Symptoms consistent with CTS were defined as tingling, numbness, burning, and/or pain in one or more of the median nerve innervated digits (17, 33). No distinction was made between symptoms occurring on the palmer or dorsal aspects of those digits. Consistent with our prior publications, an EDS was classified as abnormal and consistent with median mononeuropathy at the wrist if: (i) peak median sensory latency across the wrist was >3.7 ms or onset median sensory latency across the wrist was >3.2 ms at 14 cm, (ii) distal median motor latency was >4.5 ms, (iii) transcarpal sensory difference (ie, the difference in sensory latencies between the median and ulnar nerves across the wrist) was >0.85 ms, or (iv) no sensory nerve action potential or compound motor action potential could be elicited (17, 33). Workers meeting the CTS case definition and who also had concurrent peak ulnar sensory latency across the wrist of >3.68 ms or onset ulnar sensory latency across the wrist of >3.18 ms at 14 cm were classified as having possible polyneuropathy and right censored as non-cases.
Statistical analysis
Descriptive statistics were calculated for all variables used. Where appropriate, independent samples t-tests were used to compare differences in variable distributions between males and females. Spearman’s rank correlation coefficient (Spearman’s rho) was used to study correlation between variables. Type I (alpha) error was set to 0.05 for all analyses.
For CTS incident eligible workers, time from study enrollment to first occurrence of CTS was modeled using Cox proportional hazard (PH) regression (35). Workers lost to follow-up prior to developing an incident case of CTS were censored as non-cases on the last date they contributed data. Hazard ratios (HR) and corresponding 95% confidence intervals (95% CI) were calculated for all independent variables. PF, HAL, TLV for HAL, and age were treated as time-varying covariates. Gender, BMI, and presence of predisposing conditions were treated as time-independent covariates. We used Cox frailty models with research site as a random effect for all unadjusted and adjusted analyses to account for any variation in CTS that was unexplained by the individual exposure variables and covariates (36). Akaike information criterion (AIC) scores (37, 38) were computed for each model and used to compare model fit (39). Analyses were performed using the coxph() function in R-64 version 3.1.0 for Macintosh (40).
The functional form of each continuous variable (ie, age, BMI, PF, HAL, and TLV for HAL score) was examined using Martingale residual plots (41). The null PH model was fit and the resulting Martingale residuals were plotted against each of the five continuous variables. Smoothed plots of the residuals provided approximate shapes of the association between the log HR and a given covariate (41). Both loess and cubic smoothing splines were used as flexible means of estimating distribution shapes, as different smoothing methods may suggest different functional forms (42, 43). No transformations were suggested for any of the five continuous variables, and thus all continuous variables were treated as linear – on the logarithm of the HR scale – within the Cox regression models.
Separate unadjusted PH models with incident CTS as the dependent variable were fit with PF, HAL, PF and HAL (PF+HAL) in the same model, TLV for HAL score, and categorical TLV for HAL as independent variables. Age, gender, BMI, and presence of predisposing medical conditions were selected a priori as covariates on the basis that these have previously shown association with CTS (17) and had been used as covariates by Bonfiglioli et al (32). The independent associations between these covariates and incident CTS were estimated. Additionally, we tested for two-way interactions between age, gender, BMI, and predisposing conditions. If an interaction term from those two-way tests had P≤0.10, we included the term in the adjusted models.
Separate multivariate models were built to test whether PF, HAL, PF+HAL, TLV for HAL score, and categorical TLV for HAL were associated with incident CTS after adjusting for age, gender, BMI, comorbid conditions, and research site. Contour plots visualizing the combinations of PF and HAL associated with various HR were constructed using the regression results from the adjusted TLV for HAL score and PF+HAL models.
Because those workers with persistent, prolonged ulnar nerve latencies were no longer eligible to meet the study case definition of CTS, post-hoc analyses were performed in which all participants with abnormal ulnar latencies were censored at the time their first abnormal ulnar latency was ascertained, regardless of their concurrent median nerve latency values. An additional set of post-hoc analyses was conducted in which no worker was censored for a prolonged ulnar latency (ie, the study CTS case definition was modified to include only characteristic symptoms and abnormal median nerve latency values).
Results
Cohort description
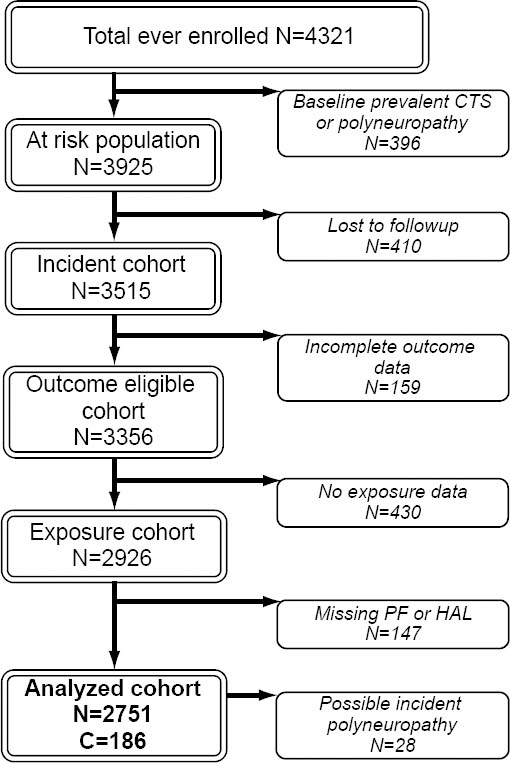
Six research sites combined data from 4321 workers, of whom 3356 had follow-up data and were eligible for inclusion in the incident analyses (figure 1). Of these, 430 participants were missing physical exposure measurements leaving 2926 workers with both physical exposure and follow-up health outcomes data. Participants missing either PF or HAL (N=147) measures were also excluded. Thus, 2751 workers were included in the current analyses; of which 28 were censored during follow-up at the time they developed possible polyneuropathy. A total of 6243 person-years of observation time were contributed over the maximum of 6.4 years of follow-up.
Descriptive statistics
At the time of enrollment, the average age of the analyzed cohort (N=2751) was 39.6 (range: 18.0–68.6) years (table 1). Approximately half the workers were female (50.9%), and the mean BMI was 28.4 kg/m2, ranging from underweight (minimum BMI=15.9 kg/m2) to morbidly obese (maximum BMI=67.7 kg/m2). On average, females were approximately five years older than males (41.9 versus 37.2 years, P<0.01), and both genders had about the same BMI. More females had one or more comorbid medical conditions (ie, diabetes mellitus, rheumatoid arthritis, or thyroid disease) than males at baseline (17.5% of females versus 6.5% of males).
Table 1
Descriptive statistics at baseline (N=2751 with 186 CTS cases). [AL=action limit; BMI=body mass index; BORG CR-10=Borg category ratio 0–10 scale rating; HAL=hand-activity level; IQR=interquartile range; PF=peak force; SD=standard deviation; TLV=threshold limit value]
During follow-up, there were 186 incident cases of CTS in this cohort with an overall incident rate of 2.98 cases per 100 person-years. The CTS incidence rate among female participants was significantly greater than among men (3.47/100 person-years versus 2.43/100 person-years, P=0.02).
Most workers (71.9%) performed mono-task jobs (ie, performed only one-task per shift) (24). Similarly, most workers (75.1%) had no change in physical exposure (compared to baseline) during the study. At baseline, mean TWA PF and mean TWA HAL were 2.9 [standard deviation (SD) 1.7, range 0–10] and 4.3 (SD 1.9, range 0–10), respectively (table 1). Males had higher TWA PF than females [3.3 (SD 1.7) versus 2.4 (SD 1.5), P<0.01]. However, females had a slightly higher TWA HAL than males [4.5 (SD 1.8) versus 4.2 (SD 1.9), P<0.01]. A weak correlation was found between TWA PF and TWA HAL (Spearman’s rho 0.29). This correlation was stronger among males than females (Spearman’s rho 0.37 versus 0.28, respectively).
At baseline, the average TLV for HAL score was 0.63 (SD 0.59, range 0–8) and males had higher TLV for HAL scores than females [0.73 (SD 0.68) versus 0.53 (SD 0.47), P<0.01]. Using the ACGIH recommendations for AL (ie, score <0.56) and TLV (ie, score >0.78), a majority of workers (55.3%) had exposures below the AL, 18.6% were between the AL and TLV, and 26.1% were above the TLV.
Unadjusted models
In this cohort, age and gender were significant risk factors for CTS. Age was linearly associated with a HR of 1.18 per decade (95% CI 1.05–1.32) and female gender had a HR of 1.46 (95% CI 1.08–1.98). A statistically significant age by gender interaction was observed; among females CTS risk increased by 32% with each decade of age (HR=1.32 per decade, 95% CI 1.13–1.52) whereas among males there was no significant effect of age on CTS risk (HR=1.00 per decade, 95% CI 0.82–1.21). BMI was linearly associated with increased risk of CTS (HR=1.05 per unit, 95% CI 1.03–1.07) and there was no interaction between BMI and gender (P=0.58). Other medical conditions were not statistically associated with incident CTS (HR=1.17, 95% CI 0.76–1.80).
In unadjusted models, both PF and HAL were linearly associated with incident CTS (HR=1.10 per unit, 95% CI 1.01–1.19 and HR=1.10 per unit, 95% CI 0.99–1.21, respectively) (table 2). When PF and HAL were included in the same unadjusted model (ie, controlling for the effect of each variable on the other) no material change in HR was observed for either variable (table 2).
Table 2
Crude and adjusted associations between peak force (PF), hand-activity level (HAL), PF+HAL, threshold limit value (TLV) for HAL score, and TLV for HAL categories and incident carpal tunnel syndrom (N=2751). [AIC=Akaike information criterion; AL=action limit]
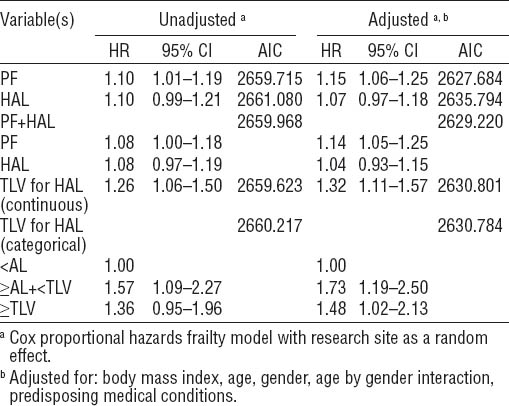
When modeled as a continuous variable, TLV for HAL score was significantly associated with incident CTS (HR=1.26 per unit, 95% CI 1.06–1.50). When categorized using the ACGIH recommended AL and TLV, participants with exposure between the AL and TLV had a HR of 1.57 (95% CI 1.09–2.27), and participants with exposure above the TLV had an HR of 1.36 (95% CI 0.95–1.96) as compared to those with values below the AL.
Adjusted models
The adjusted models included BMI, age, gender, an age×gender interaction term, other medical conditions, and research site. In general, the addition of these covariates improved the strength of association between physical exposure and incidence of CTS (table 2). The exception was HAL, where the strength of the association was reduced, both in the HAL-only and PF+HAL models. In adjusted models, the HR of PF increased, and the HR of HAL decreased such that unitary increase in risk for PF was approximately twice that of HAL (15% versus 7%, respectively). Similarly, in the adjusted PF+HAL model, the unitary increase in risk for PF was approximately 3.5 times greater than the unitary increase in risk for HAL (14% versus 4%, respectively) (table 2).
AIC scores for the adjusted models improved by an average of 29.4 points (range 15.4–32.2) over the unadjusted models. Among the five adjusted models, the PF model had the lowest AIC score; however, the adjusted PF+HAL model was within two AIC points of the adjusted PF model and thus these two models had comparable fits (39). The AIC score of the adjusted HAL model was approximately eight points higher than the adjusted PF model indicating a relatively poor fit compared to the other models (39).
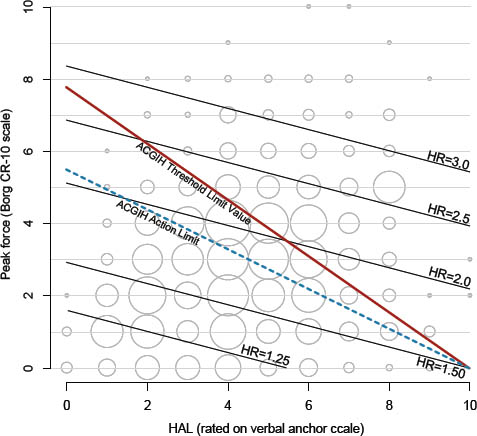
Figures 2 and 3 show contour plots of HR for the adjusted PF+HAL model and the adjusted TLV for HAL continuous model respectively, as compared to the recommended ACGIH AL and TLV lines. These figures also contain bubble plots showing the distribution of combinations of PF and HAL within the cohort (bubble areas are proportional to sample size). These figures show combinations of PF and HAL that produce the same risk (relative to unexposed) using results from the PF+HAL and the continuous TLV for HAL models. The adjusted PF+HAL model reveals that the risk increases uniformly (ie, parallel HR lines) with a slope of approximately -0.30 (figure 2). On the other hand, the adjusted continuous TLV for HAL model shows the risk increasing radially around the fixed intercept of HAL=10.
Post-hoc analysis
In the post-hoc analyses, when those with abnormal ulnar latency (N=207 workers) were censored at the time the abnormal measurement was ascertained, the HR for both unadjusted and adjusted models increased between 1–6% with the exception of the “above TLV” category which increased by approximately 17% in both models. Additionally, 95% CI narrowed modestly for all models.
Conversely, when those with abnormal ulnar latency at the time of incident CTS were retained as CTS cases (N=28 additional cases), rather than censored as having possible polyneuropathy, the HR for both unadjusted and adjusted models decreased by between 1–5% with the exception of the between AL and TLV category, which decreased by 9% in both models. Changes in 95% CI widths were negligible for all models.
Discussion
The TLV for HAL is a useful tool for screening jobs for distal upper-extremity injury risk prediction. It is relatively easy to learn and quick to apply (28). The findings of this prospective study and the prospective study of Bonfiglioli et al (32) provide insights into the exposure–response relationships between the TLV for HAL model – and the PF and HAL variables within – and incidence of CTS. These findings should be helpful to both industry and governmental agencies as they evaluate, design, and modify jobs, and set physical exposure policies to help prevent MSD. While the findings of this study are broadly consistent with those of Bonfiglioli et al (32) and other studies that have shown an association between the ACGIH TLV for HAL and incidence of CTS in occupational settings (16, 23, 25, 29–31), there are some noteworthy differences.
ACGIH recommended AL and TLV as risk factors for CTS
Our analyses of the TLV for HAL model showed increased risk of CTS for exposures above the AL. However, contrary to the findings of Bonfiglioli et al (32), we did not observe a further increase in risk when participants were exposed above the TLV. Nevertheless, both studies show a marked increase in risk for those with exposures between the AL and TLV as compared to those with exposures below the AL. Thus, our findings support the conclusion of Bonfiglioli et al: the current AL does not appear to be sufficiently protective of workers.
The lack of further increase in risk above the TLV is unexpected, but possibly explained by a healthy worker survival effect (44) and/or a differential bias associated with the use of PF. Regarding PF, under certain circumstances, it may not adequately represent the true distribution of forces within a task. For example, when PF is relatively low, the distribution of forces within the task is necessarily narrow and the force distribution can probably be effectively characterized by PF. However, when it is relatively high, the frequency and duration of PF may be low, and the distribution of forces within the task could be wide. In this circumstance, using PF would likely overestimate the true force distribution. An over-estimation of force might result in misclassification of risk, unless risk of injury is disproportionally increased with high, but infrequent applications of force. Though presumably easier to identify and quantify than “overall” or “typical” force (24), some consideration should be given to whether PF is a suitable estimate of the underlying force distribution when studying complex tasks with substantially varying force levels.
PF and HAL as risk factors for CTS
In the unadjusted PH model that included both PF and HAL simultaneously as independent variables (PF+HAL model), the effect sizes of PF and HAL were identical (HR=1.08 per unit). However, in the adjusted model, the HR for PF and HAL were 1.14 and 1.04, respectively. Thus, after adjusting for age, gender, BMI, research site, and predisposing conditions, a one-unit change in PF has the same effect on the HR as a 3.3-unit change in HAL (figure 2). This indicates that, per-unit change, PF had a greater effect on CTS incidence than HAL within this cohort. These findings are different than those of Bonfiglioli et al (32), where both PF and HAL were associated with CTS, but a one-unit change in HAL had the same effect on CTS incidence (using the same CTS case definition) as an approximately 3.2 unit change in PF. An examination of the distribution of PF and HAL combinations in the Bonfiglioli et al (32) study suggests that the minimum force threshold required for a HAL “hand exertion” may have been higher in their study than ours and thus their HAL variable may have included, to some degree, a latent measure of force. The notion of a minimum threshold force being needed before an effort should be counted towards repetition is consistent with separate findings from our cohort where, when repetition was quantified using video analysis, we found increased risk of CTS to be associated with “forceful repetition” but not “total repetition” rate (45). Overall, these findings suggest that increased risk associated with repetition is dependent upon the underlying forces required to perform those repetitive efforts. Studies reporting an increased risk for repetition-based measures alone may have, either by design or job sample distribution, incorporated a minimum force threshold for an exertion to be counted towards repetition.
Exposure–response relationships for combinations of PF and HAL
Equations that relate two or more physical exposure variables together into a single metric, or score, can help practitioners and researchers quantify physical exposure and risk. Practitioners can use the scores to identify high-risk tasks and prioritize ergonomics interventions, and researchers can use them to elucidate the shape and magnitude of exposure-response relationships. The ACGIH TLV for HAL model is based on the following equation to quantify the MSD risk associated with combinations of PF and HAL:
score1 = PF/(10-HAL) (equation 1a)
In equation 1a, “10” refers to a fixed intercept of HAL=10 (on the x-axis) at PF=0 and score is the slope of an equal risk line (figure 3). For the ACGIH TLV for HAL, the slope of the AL is (-) 0.56 and for the TLV is (-) 0.78. Figure 3 shows equal risk lines using the results from the adjusted TLV for HAL continuous model of table 2. HR for any given value of score1 can be calculated using equation 1b.
HR=1.321(score1) (equation 1b)
Allowing the HAL intercept to vary yields different risk contours for combinations of PF and HAL (figure 2). The PF+HAL statistical model, used to define the equal risk contours in figure 2, leads to these alternative equations:
score2=C1×PF+C2×HAL (equation 2a)
HR=1.141(score2) (equation 2b)
Where, C1 and C2 are constants that define the slope of the equal risk contours and score is the intercept where an equal risk contour meets the y-axis. The slope can be defined graphically by plotting predicted HR, or by taking the ratio of the regression coefficients of HAL and PF. Based on the results in table 2, the slope of the equal risk contours is -0.30, calculated from [-log(1.04)/log(1.14)], and thus C1=1.0 and C2=0.30 for our cohort.
Figure 3
Contour plot of hazard ratios (HR) for combinations of peak force (PF) and hand-activity level (HAL) based on the results of the adjusted threshold limit value (TLV) for HAL as a continuous variable model.
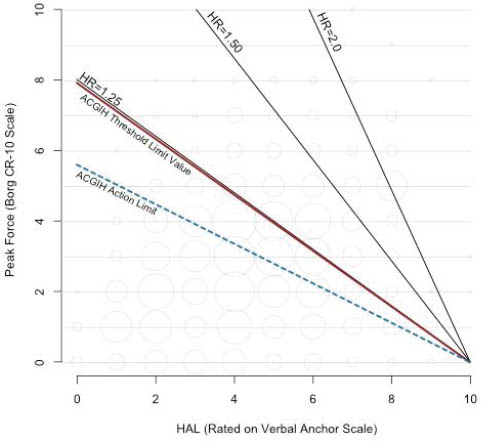
Figures 2 and 3 show that these two mathematical constructs yield different HR for the same combinations of PF and HAL. Further investigations are needed to explore the effect of: (i) altering the location of the fixed intercept in equation 1a, (ii) altering the coefficients of equation 2a, and (iii) potential statistical interactions between PH and HAL. From explorations such as these, it may be possible to determine the best mathematical construct for the relationship between PF and HAL pertaining to increased CTS risk and the optimal location of the AL and TLV lines.
Current exposure as a measure of CTS Risk
We used current physical exposure as the measure of risk for developing CTS, consistent with the assumptions made in many recent epidemiological studies (16, 19, 23, 25, 29–32). However, it is possible that CTS is a consequence of accumulation of physical exposure over a period of time, and there is a lag-time between the beginning of exposure and development of the disease (46). If true, this would suggest that cumulative physical exposure might be a more appropriate measure of CTS risk. Unfortunately, simple accumulation of exposure with time considers the effect of a unit increase in exposure (eg, force) identical to a unit increase in exposure time, an unlikely relationship (47). Further, no reliable information is available on what the lag-time for development of CTS might be, thus it is impractical to make an a priori assumption about how long to lag prior exposure following a change of job. Future research is needed on appropriate measures of cumulative exposure and lag time for development of occupational injuries and diseases such as CTS.
Limitations
These analyses of combined raw data increase statistical power over the individual studies comprised within and increase generalizability by aggregating a diverse workforce employed in numerous manufacturing and service occupations in several US states (24, 33). Despite these advantages, data pooling also has some noteworthy limitations. Perhaps the most significant of these are the differences in data collection methods between studies. None of the research groups directly collaborated prior to the combining of data and thus no workers or jobs were simultaneously included in data collection but rather under multiple protocols and, in turn, no objective comparisons of measurement reliability, sensitivity, and specificity between sites can be made. With regard to the rating of PF and HAL, we believe that individual site data collection methods were reasonably comparable because analysts received similar training. Nevertheless, if the true interanalyst reliability between sites was poor, it would be expected to result in underestimates of effect and strengths of association. We used frailty models with research site as a random factor for all analyses (both unadjusted and adjusted) to account for otherwise unmeasured methodological differences, background exposure differences, or other unexplained demographic or regional differences between research sites. However, it is possible that the research site variable is associated with both physical exposure differences and health outcome differences between research sites and thus might have over-controlled for site effects and led to underestimates of true associations. We were unable to include psychosocial variables as covariates due to marked differences in how each site measured psychosocial factors. Thus, we cannot provide insight into how these potentially important factors affect the association between the TLV for HAL and CTS. In addition, most workers in the study had been employed in manual labor occupations for several years prior to study and likely represented a less susceptible, survivor population (48). Therefore the effect sizes shown in these results may be somewhat lower than what would have been found in a population of new hires (48). Finally, the findings presented were from analyses in which workers with possible polyneuropathy were censored at the time they would otherwise have become a CTS case. Given limitations of resources, the only evidence of polyneuropathy among participants available for inclusion in the analysis was the observation of prolonged ulnar nerve latency. However, post-hoc analyses showed that changing the study criteria to either (i) censor those with abnormal ulnar nerve latency at the time that it was ascertained or, (ii) retain, rather than censor, incident CTS cases who also had a prolonged ulnar latency had no material effect on the strength of the observed associations nor on the conclusions of this study.
Concluding remarks
The ACGIH TLV for HAL is associated with increased incidence of CTS, both when treated as a continuous measure, and when classified using the current AL and TLV. The results of this study appear to confirm the assertion of Bonfiglioli et al (32) that the current AL may not be sufficiently protective of some workers and should probably be lowered. With regard to PF and HAL, we found both to be associated, within this cohort, with increased incidence of CTS, but PF had a relatively larger effect on risk than HAL. These results contribute to the growing body of literature suggesting that applied hand force is an important risk factor for CTS and that combinations of PF and HAL can be effective predictors of high-risk jobs.