In occupational epidemiology, there is significant interest in analyzing causal relationships between work-related factors, socioeconomic status, and health. This interplay has a dynamic relationship during the life course of a worker (1, 2). In that sense, in a changing labor market, cross-sectional designs fall short because they capture health and work status only at one moment in time and do not provide any information on previous work life and health status. Researchers with access to repeated measures should explore which methodologies can adequately address research questions that include time-varying data.

Recently, computational advances and the large amount of data that administrative systems are continuously collecting allow the use of statistical techniques that have the potential to obtain more interesting and reliable results. The Spanish social security system collects longitudinal information related to work and pensions, dating back to 1981. This information includes repeated measures of variables with exact dates in time, which is useful for research on the role of employment and employment-related events over the life course and their relation to worker health. More specifically, access to repeated measures allows the construction of working life trajectories (WLT) by one key variable, such as employment time, allowing us to examine the pathway an individual follows over a lifetime. This approach is relatively novel in occupational health research. At a population level, we are then able to group individuals with similar WLT, enabling the study of the associations between different trajectories, other determinants like socioeconomic status (SES) and outcomes such as permanent disability or mortality. Although there are several statistical approaches to obtain heterogeneous trajectories, our work focuses on one of them, namely latent growth modeling (LGM) (3, 4).

LGM techniques represent a flexible statistical approach for longitudinal data to capture information about interindividual differences in intraindividual changes over time taking into account unobserved heterogeneity within a larger population (3, 5, 6). This allows us to represent unobserved heterogeneity by means of separate growth models for each latent class (trajectory), each with its unique estimates of variances and covariate influences. There are two similar LGM approaches to this end: growth mixture modeling (GMM) (7, 8) and latent class growth analysis (LCGA) (9). GMM can be described as a multilevel, random-effects model that allows for variability in the growth factors within each class (variance and covariance). On the other hand, LCGA is a special type of GMM in which random effects (variance and covariance) for the growth parameters within each trajectory are assumed to be fixed at zero, and considers all individuals in a trajectory as homogeneous (10, 11, 12). In this sense, GMM depicts more accuracy in terms of discriminating individuals within a trajectory. However, large datasets may benefit more from LCGA as convergence is more stable and requires a lower computational workload. This feature makes LCGA more appropriate when dealing with complex models (3, 4).

The application of LGM in the field of occupational health is currently growing and becoming popular (1). These approaches have mostly been used to capture unknown heterogeneity in work-related factors and to see their association with some health outcomes. For example, to study the association between occupational complexity and cognition in later life (13), work characteristics and hypertension (14), absenteeism trajectories and health factors (15), or work functioning and return to work after sick leave (16), among other similar studies (17, 18, 19, 20). In summary, these approaches allow us to address labor market changes from a life course perspective (21).

The aim of this study was to describe the application of LCGA to identify different WLT using employed working time by year as a repeated measure, taking advantage of the Spanish WORKing life Social Security (WORKss) cohort (22).

Methods

Statistical analysis

To construct the WLT, we built 32 measurement periods for each participant, one per year of observation (1981–2013) containing the days worked. We introduced zero working days if the person was inactive during a certain year but had an administrative activity before and after that period. If individuals were not working a certain year due to permanent disability, early retirement or death, a missing value is coded because in these situations the individual is not able to work. We used LCGA to identify different WLT.

Trajectories can be estimated assuming they follow any equation, either a linear function, a quadratic function or any expression including more complex elements. The number of these parameters, called latent growth factors, can vary according to the data, but it is recommended to apply the criterion of parsimony and use the fewest number of parameters to obtain similar results. Figure 1 features the LGM representation consisting of j latent growth trajectories with three latent growth factors, intercept (I_j), slope (S_j) and the quadratic growth factor (Q_j), formed by the observed variables that represent repeated measures across 32 time points (1981–2013).

Figure 1

Representation of a latent class growth analysis assuming three latent growth factors: intercept I_j, slope S_j and quadratic element Q_j.

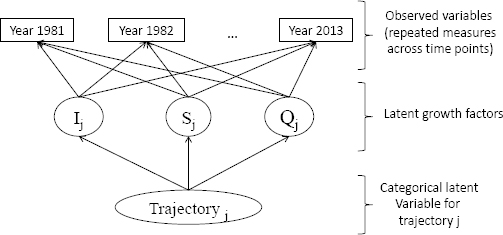
As individuals are assigned in the different trajectories according to the highest probability of belonging to each one, trajectories can also be constructed calculating the mean of yearly worked days for all the individuals within each trajectory. So two types of trajectories can be constructed: on the one hand, the estimated WLT by means of the latent growth factors, intercept (I) and slope (S) in this case and, on the other hand, the observed WLT by calculating the mean of days worked. Both are presented so that the fit of the estimation can be compared to the observed values.

There are different criteria for assessing the optimal number of latent trajectories. On the one hand, an initial approach can be based on prior knowledge of the researcher. On the other hand, a combination of fit indices can be considered, such as the entropy (near to 1), a significant Lo, Mendell and Rubin likelihood ratio test (LMR-LRT) or a significant bootstrap likelihood ratio test (BLRT). The LMR-LRT and BLRT tests provide information to avoid overestimation of the number of trajectories. In particular, these two tests allow for the comparison of model fit between subsequent models, and then a significant P-value suggests that a model with one more trajectory provides better results in terms of goodness of fit. Model fit can be also assessed with the Akaike information criterion (AIC), Bayesian information criterion (BIC) and the sample-size-adjusted BIC, with the lowest values indicating the best model (24). In addition, other elements can also help specify the number of trajectories, such as parsimony, a theoretical justification, successful convergence, high posterior probabilities (near 1.0) or interpretability (eg, classifying <1% of individuals in one class may make no sense) (25, 26, 27).

Results

We began the analysis using two latent growth factors (the intercept and the slope) and then repeated our analysis also considering the quadratic factor. The representation of the trajectories was nearly identical, so we selected the more parsimonious approach using only the two latent growth factors (the corresponding A in table 1).

Then, after testing different models with these two latent growth factors (group A of WLT), we began building a model with two trajectories, then three trajectories and so on until an optimal number of trajectories was identified. The model with at ≥5 WLT was identified as the probably best solution according to the fit indices. The AIC and BIC indices were the smallest, the LMR-LRT and BLRT indices were statistically significant regarding to subsequent models and, lastly, the entropy index was >0.95, as in the other models. However, when comparing the graphical representation using WLT4 and WLT5 (Figure 2), the additional WLT (WLT5 in the bottom Figure 2) shows a slope similar to that of WLT3. Therefore, we decided to select WLT4 because we felt WLT5 did not provide enough information to sufficiently justify its inclusion, based on our previous knowledge of the Spanish labor market.

Figure 2

Observed and estimated growth trajectories considering the annual number of worked days (1981–2013) among people from the sub-sample of the Spanish WORKing life Social Security (WORKss) cohort, limited to individuals born 1956–1965 (N= 247 477). On the top, four working life trajectories (WLT) are represented and on the bottom, five WLT.

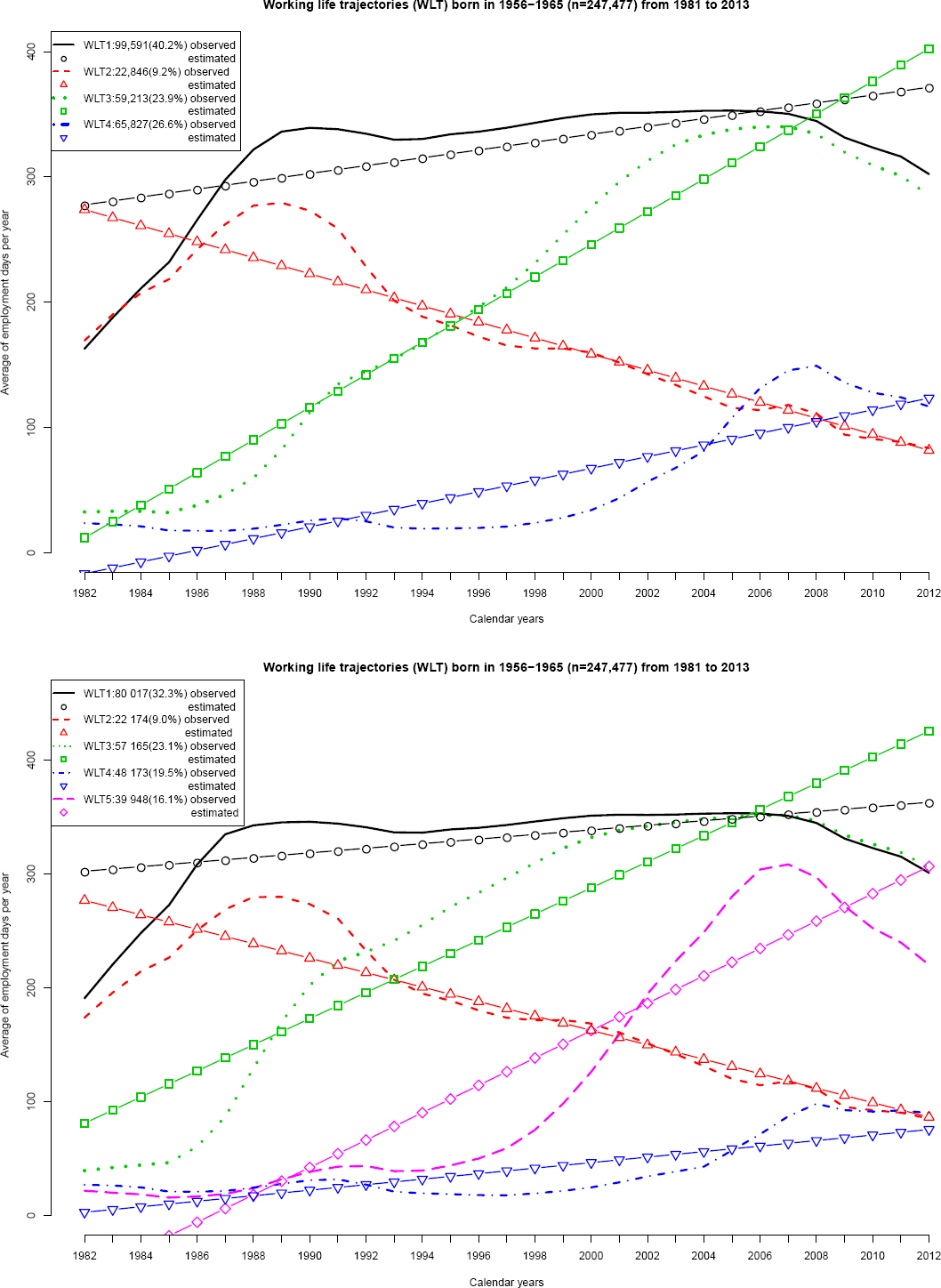
The four trajectory models were roughly classified as: WLT1, people who were employed most of the time (N=99 591; 40.2%), or “high labor force participation”; WLT2, people with an average number of worked days (around 200 days per year) including a peak around 1989 and decreasing afterwards, or “decreased labor force participation” (N=22 846; 9.2%); WLT3, people who worked for a few days in the 1980s but increased the days worked during the rest of the study period (N=59 213; 23.9%), classified as “increased labor force participation”; and WLT4, people who mostly did not work during the analyzed years except for an increase around 2005 (N=65 827; 26.6%), or “low labor force participation”.

Table 2 describes the four trajectories considering sex, mean age, number of years worked, occupational category. Regarding sex, the decreased and increased labor force participation trajectories contained roughly the same proportion of men and women and had more or less the same distribution of people in each category of years worked. Men (73%) dominated in the high labor force participation and women (63%) dominated in the low labor force participation trajectory. As expected, the high labor force participation trajectory mostly included individuals with >19 years of work experience, whereas the opposite occurred in the low labor force participation trajectory. When occupational category was considered, no such differences between trajectories were present, except for increased and low labor force participation, both of which included a lower percentage of non-manual skilled workers.

Discussion

LGM approaches are a powerful statistical tool for identifying different latent trajectories, which in turn allow the classification of individuals into specific trajectories. From a life course perspective, this categorization enables the identification of different patterns shaped by working lives over time rather than focusing in cross-sectional studies. Thus, taking advantage of longitudinal data on working people, LGM approaches allow the identification of different labor paths rather than looking at individual evolution over time. In this study, we focused on LCGA and applied it to a subsample of the Spanish WORKss cohort, which provides data based on a 32-year follow-up period. Before LCGA we used GMM, but we encountered convergence problems due to the high number of parameters based on 32 time points (28).

Besides identifying different trajectories, LCGA also assigns each individual to the WLT to which they have the highest probability of belonging. This classification produces a new variable that was not so easily managed before applying the LCGA. This new variable can then be included in a subsequent analysis as a categorical explanatory variable where each trajectory would be a category of the variable. The idea is to assign a latent class to each individual in a sample, adding a new variable to the original dataset that incorporates latent information not previously available.

WLT were summarized into four categories based on differences in their slopes. The “high labor force participation” trajectory was the one with the greatest number of worked days and a low positive slope and included the largest percentage of individuals in the sample (40.2%), most of whom were men. This trajectory could be described as the one with a stable working life trajectory because individuals had been working most of the time. In fact, the trajectory with the lowest percentage (9.2%) corresponded to the “decreased labor force participation”, which was the only one with a negative slope and composed mainly of women. Differences regarding sex could be explained by the fact that our study sample represents a period of time where women had a low participation rate in the Spanish labor market. Their participation increased at the end of our follow-up period (29). The two remaining trajectories, with small differences regarding sex, showed positive slopes that had similar starting values; however, one increased much faster than the other one. Finally, it is worth mentioning that the occupational category did not have a strong influence in the results. This may be due to the period covered by the data; a period of economic expansion which brought a wide demand of all different occupational categories. These results showed a positive trend as most of individuals in the sample, about 90% of workers included in these trajectories increased the days worked per year as time elapsed.

The decision about the number of trajectories was based, in the first and main step, on the classification accuracy values, but also, in a second and complementary step, on the representativeness and distinctiveness of the trajectories, driven by the knowledge and experience of the researcher. Combining statistical criteria with expert knowledge was felt to be the best way to identify the optimal model.

The challenge here was to classify individuals with similar workloads over time into different groups, resulting in a new categorical variable that we called WLT. In our study, these LCGA-identified WLT were explicitly based on the days worked each year. However, other WLT could have been identified if we had used other variables included in the dataset – such as the number of contracts or the time in unemployment – as the independent variable. Furthermore, other variables not included in the dataset (eg, the number of children) or other information that we are not even aware of (eg, the distance between place of residence and work) could influence the heterogeneity identified by LCGA. Certainly, these unknown variables can be relevant if they are associated with health outcomes of interest according to our hypothesis.

The LGM literature includes several studies that have used the methodology described in this paper for the analysis of repeated measures data for the purpose of identifying individual trajectories given certain variables (8, 13, 14, 30, 31). In an occupational study, Raymo et al (2) identified latent class employment trajectories using the probability of being employed; the trajectory patterns they identified were quite similar to ours, but none centered on the analysis of WLT as we have done. To our knowledge, this is the first study focused on the construction of WLT. In particular, we identified different working latent trajectories over time considering the average number of worked days per year in a representative sample of a country workforce. In addition, this study was based on a large dynamic cohort with a large number of independent measures.

Our dataset presents a left-sided truncation as we only considered persons who had contact with the social security system in 2004–2013. We were not able to collect data on those who did not have contact within this period. Thus, for example, the last part of the WLT4 might have been flatter if we had been able to observe people in contact with the social security system prior to 2004. It is likely that these persons did not work during the period 2004–2013 and, thus, the average number of days worked per year would have decreased and the trajectory would have been lower.

Another limitation is the absence of information on informal employment, defined as workers lacking social security protections (32). Thus, the WLT we identified only represent those Spanish workers who had a formal contract and were eligible for social protection. Moreover, we estimated the trajectories based only on the number of days worked per year. Other factors, such as the number of new entries into the workforce or annual number of contracts, could also be interesting for classifying each individual as a reflection of the flexibility experienced in trajectories. For example, it is not the same thing to be employed for a similar number of days with one versus four contracts.

Longitudinal data that are regularly collected by administrative systems can benefit from LGM approaches to identify different trajectory patterns that may be associated with an outcome of interest. In occupational epidemiology, this study provides a step forward by using this modeling approach to identify different WLT. Examining the effect of these WLT on health outcomes may be useful in the design of prevention policies. However, there is a dynamic relationship between the heterogeneity identified by LGM and many known and unknown time-varying determinants that is not easy to interpret. Accessing information of work, socioeconomic status and health on the same individual over time is of paramount importance to control, as much as possible, whether statistical effects are due to causality or bias (33). More complex LGM is needed to more properly analyze the issues this study raises.