In a recent commentary (1) on a large (N=197 473) individual participant meta-analysis of job strain and incident coronary heart disease (CHD) (2), it was suggested that the population attributable risk (PAR) was smaller than expected (3.4%). And while this issue was addressed by the original authors (3), the present comment expands the discussion by taking a closer look at data presented in the supplemental material (4), indicating that there is an alternative model based on job control with a larger estimated PAR (8.5%).
The job strain model is a stress theory based on two dimensions describing job demand and job control (5). It is usually studied by comparing groups split at the study-specific median of both dimensions to form four quadrants (2). The quadrant characterized by high demand and low control is called job strain. Based on this theory there are four competing models:
-
Job demand but not job control is associated with CHD.
-
Job control but not job demand is associated with CHD.
-
Job demand and job control are both independently associated with CHD. This has sometimes, a bit confusingly, been called an “additive interaction” in the literature (6). It describes two additive associations needed to predict all four quadrants of the model and is tested for statistical significance by simultaneously fitting terms for both job demand and job control in the same model.
-
Job control modifies the association between job demand and CHD (or vice versa). This describes a true interaction with a unique estimate for all quadrants in the model and is tested for statistical significance by adding an interaction term, multiplying job demand with job control, to model 3 above.
Unfortunately, none of the four models above were presented in the report (2). Instead, the authors opted to create a binary job strain variable for the analyses. However, since it combines both exposures (low job control and high job demand) into a single variable, it is susceptible to show a significant association when any of the four models above is correct, including model 1 or 2, making it unsuitable for testing any specific hypothesis.
The authors did provide some additional information in the supplemental material (4). In table S1 they present hazard ratios (HR) for a linear exposure as well as for three quartile groups (Q2-Q4) compared to a reference group (Q1) separately for both job demand and job control. No significant association was observed for job demand, but both the linear exposure model and the model with quartile groups indicated significantly increased HR for low job control, which is consistent with model 2 above.
Model 1 and 2
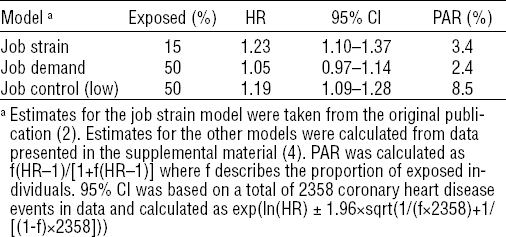
It is possible to calculate the HR of the original (median split) job control variable from the quartile data. Since the groups are equally sized and the top two quartiles (Q1 & Q2) were both estimated with a HR of 1, a good approximation of the HR using both Q1 and Q2 as the reference for Q3 (HR=0.89) and Q4 (HR=0.80) combined is the mean of the two calculated as exp((ln(0.89) + ln(0.80)) / 2) which gives a protective HR of 0.84 for high job control. Inverting the estimate gives a HR of 1.19 for exposure to low job control that is easier to compare with job strain. The HR for job demand were estimated at HR 1, 1.05, 1.08, 1.07 respectively for Q1–Q4 and were also used to calculate a HR for a median split model exp((ln(1.08) + ln(1.07)) / 2) / exp((ln(1) + ln(1.05)) / 2) = 1.05 providing all the information needed to calculate the population attributable risk (PAR) for model 1 and 2 mentioned above, using the same equation as the original publication, and compare it to the proposed job strain model.
The results are summarized in table 1 and confirm that job demand was not associated with CHD. The HR for job control was estimated slightly smaller than for job strain, but because many more individuals were exposed to low job control, PAR was estimated much higher at 8.5% compared to only 3.4% for job strain.
Model 4
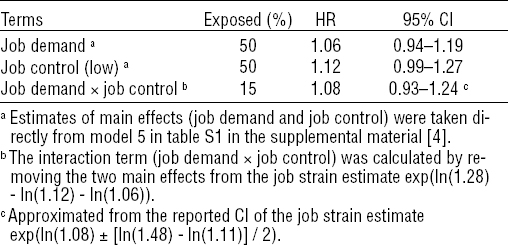
Unique estimates for all quadrants of the model were also presented in the supplemental material (4). This is equivalent to model 4 above but with a different parameterization without an interaction term. The estimates for high job demand HR 1.06 [95% confidence interval (95% CI) 0.94–1.19] and low job control HR 1.12 (95% CI 0.99–1.27) were not significant. The combination of these two is called job strain and showed a HR of 1.28 (95% CI 1.11–1.48). We can find the interaction term by removing the two main effects of job control and job demand from the job strain estimate exp(ln(1.28) - ln(1.12) - ln(1.06)) which gives a HR of 1.08 for the interaction. And we can approximate a 95% CI for the interaction term based on the reported CI of job strain exp(ln(1.08) ± (ln(1.48) - ln(1.11))/2) which gives a non-significant 95% CI for the interaction term of 0.93–1.24. The full model is summarized in table 2 indicating that model 4 was not supported by data.
Model 3
We cannot directly test model 3 on the published data. However, from the small and nonsignificant interaction term presented in table 2, we can infer that the estimates for job demand and job control would only change marginally if the interaction term was removed from the model. If we assume that the small “effect” described by the interaction (HR 1.08) would be evenly distributed over two (high job demand and low job control) larger (0.50/0.15=3.33) groups, we would expect to see the job demand estimate increase from HR 1.06 to approximately exp(ln(1.06) + ln(1.08)/2/3.33)≈1.072 which is unlikely to show a statistically significant 95% CI, though such conclusion should be verified by actually fitting the model on data.
Concluding remarks
A closer look at the published data from a large individual participant meta-analysis (2) suggests that the reported association between job strain and CHD might be fully explained by low job control. This issue can be resolved by fitting models 3 & 4 on data. The data also showed that job demand was not associated with CHD and that combining it with job control to form an exposure of job strain reduced the PAR to less than half (3.4%) of that of job control alone (8.5%). These results suggest that more focus should be put on understanding low job control as a risk factor for CHD rather than job demand or job strain.