The main source of evidence concerning the carcinogenicity of occupational hazards in humans is obtained via epidemiological studies among workers, and one of the main criteria for establishing a causal link is the existence of dose–response relationships. Historically, most of dose–response relationships have been obtained in cohort studies of workers who are, if not solely, usually predominantly exposed to a single carcinogen. For instance, in the recent IARC classification of diesel motor exhaust (DME) as a group 1 carcinogen, the cohort studies (1, 2) – in which exposure had been accurately determined and a dose–relationship observed – have carried great weight. Population-based case–control studies have been less successful in identifying dose–response relationships. This might be due to the fact that exposure cannot rely on measurements carried out in the actual workplace and must be estimated indirectly. Most population-based case–control studies that managed to identify dose–response relationships relied on expert-based exposure assessments [see eg, (3, 4)].
This possibly reflects the fact that experienced experts are able to synthesize the different types of available information (job, industry, time-period, task descriptions, use of protective devices, self-reported exposure, etc.) into meaningful quantitative exposure levels. However, expert time is rare and costly, thus expert-assessment is often obtained only for subsets of subjects. So-called 2-phase designs (5) allow an efficient choice of such subsets as was repeatedly shown from a theoretical as well as applied point of view (6–8). Briefly, in 2-phase studies, the full dataset (the phase-1 dataset) is stratified on the case–control status and exposure estimates available at this stage. Within these strata, possibly unequal fractions of cases and controls are selected for further data collection (phase-2 dataset). In the present case, this second data collection is a detailed expert assessment. The statistical analysis makes use of these sampling fractions and thus uses not only the phase-2 data but also the phase-1 information, thereby adding additional power, see for example (9). Moreover, this design allows oversampling of the most informative subjects, ie, those subjects with the rarest disease-exposure combinations.
Despite these properties, this design is quite uncommon in the epidemiological literature and in the field of occupational epidemiology, we know only of one previous paper (9). In the present paper, we aim to show the power and the feasibility of the 2-phase case–control (2PCC) design in making efficient use of expert time in the context of occupational epidemiology and on the basis of an actual lung cancer case–control study. Moreover, we present some new developments in computing the attributable fractions for this design.
Methods
Phase-1 case–control study
The study, which is the basis of our paper and which constitutes phase 1 of our 2PCC, is a population-based lung cancer case–control study in Northeast France. Details of the data collection and the population have been presented elsewhere (10). The ethics committee of the French data protection agency approved the study. Briefly, all the hospitals located in this area were contacted and agreed to declare their incident lung cancer cases. Cases were eligible if: (i) male and between 40–80 years old, (ii) resident in the study region, (iii) lung cancer was histologically confirmed, and (iv) written statements of informed consent were provided. Of 548 identified lung cancer cases, 246 were interviewed between 2006–2010.
Eight hundred male controls, aged 40–80 years, stratified on 10-year age classes and broad socioeconomic class and selected by a random digit dialing procedure in the study area, agreed to be contacted. Of these, 531 finally accepted to be interviewed.
All the cases and controls were contacted by telephone and interviewed at home in a face-to-face interview mainly focused on their occupational exposure, smoking, and disease history. Occupational exposure was first assessed by obtaining a lifelong list of all jobs held for three or more months. For each job, a general exposure questionnaire and, if relevant, one or more detailed exposure questionnaire specific to 20 jobs or activities were applied. Finally, a list of 47 task-specific questions was applied to the whole job history independently of any job code. Bourgkard et al (11) gives further details on this approach and its validity. For each job, a rule-based exposure level in four categories was assigned to each job for asbestos and polycyclic aromatic hydrocarbons (PAH) based on the task questionnaire and for crystalline silica based on the general and specific questionnaires. Cumulative exposure scores were computed multiplying this level by job duration and exposure frequency and summing them up over the job history.
Setting up the two-phase study design
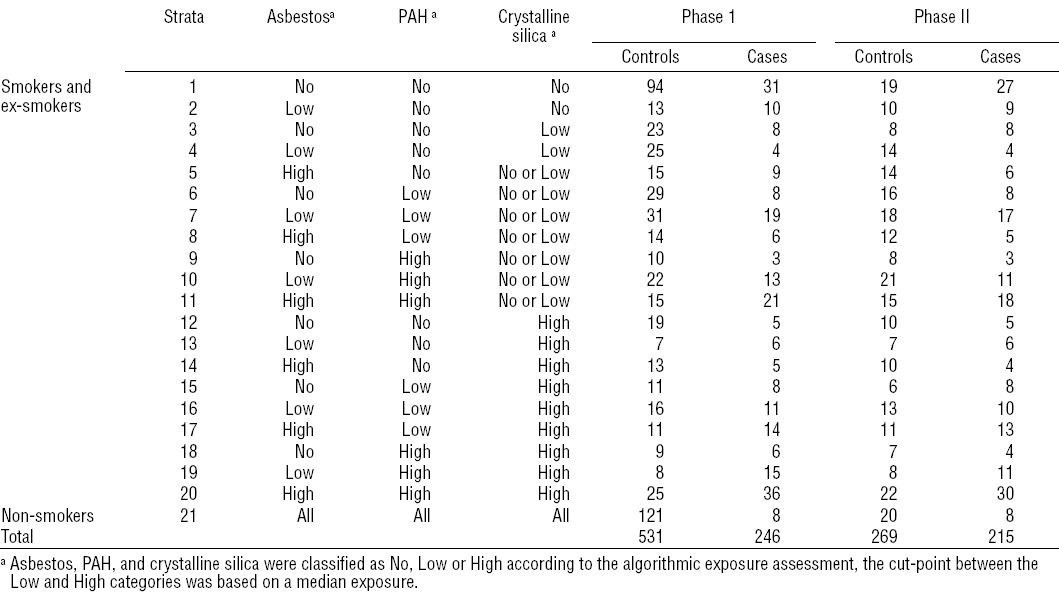
The 2-phase study was designed following the approach described in Schill et al (12). First, a stratification summarizing the exposure variables of interest was set up, cross-tabulating smoking and the three rule-based exposure scores. The first stratum was defined by never smokers whatever the exposure scores. Smokers were cross-classified by the algorithmic cumulative exposure scores of asbestos, PAH, and crystalline silica, each in turn divided into non-exposed, lower than the median score, and higher than this median. Finally, some of these strata were collapsed owing to small numbers, resulting finally to 21 strata.
Second, the stratum-specific numbers of cases and controls were chosen (table 1) for inclusion in phase 2. We wanted to be able to assess simultaneously the four main occupational carcinogens and some confounders so that virtually all cases and half of the controls were selected with approximately equal numbers in each stratum as suggested by (6). It should be noted that equal numbers correspond to very different sampling fractions in cases and controls. Phase 2 is thus deliberately non representative of phase 1, but representative within each stratum.
Phase-2 data collection: expert exposure assessment
For the cases and controls selected, two industrial hygiene experts, blind to the case–control status and the algorithmic exposure evaluation, coded the exposure to a pre-defined list of potential occupational carcinogens: asbestos, man-made mineral fibers, painting, PAH, crystalline silica, mild steel welding fumes, stainless steel welding fumes, iron mining, painting, strong acids, and DME. These exposure codes were based on all the available information in the questionnaires. The experts summarized the exposure at individual level to each of the carcinogens as a series of homogeneous exposure periods with an exposure frequency, a semi-quantitative exposure level in four increasing categories and duration in years. As in the algorithmic step, a cumulative exposure score was computed for each exposure period. These cumulative exposures were log-transformed after adding one so that non-exposed subjects had a zero log-transformed exposure. Discordant cumulative scores were identified and a second panel of three senior experts provided a final expertise obtained in consensus. Finally, for each potential carcinogen, we computed a final exposure estimate. If the initial expert assessments were consistent, this estimate was the mean of the log-transformed cumulative exposures of these two experts. If not, the exposure estimate was the consensus estimate of the second panel.
Statistical analysis
The statistical analysis was based on logistic regression adapted to 2-phase data. We chose the maximum likelihood approach as it is the more powerful. An alternative would have been the weighted likelihood approach, which is less sensitive to misclassification. Basically, these methods consist of modelling the detailed phase-2 data in a logistic regression weighted by stratum-specific ratios of numbers of subjects in phases 1 and 2. When using maximum likelihood, these weights are adjusted according to the model used (13). We used the SAS/IML® package (14). We also developed attributable fraction computations adapted to 2-phase studies, extending work by others (15, 16), in order to be able to estimate within this design the overall public health burden due to these occupational exposures. Mathematical details and a freely available add-on to the above-mentioned SAS software are available at http://tinyurl.com/schill-af2p.
The logistic regression model included as independent variables the confounders selected in the prior analysis of the full phase-1 data, with the exception of wine drinking whose borderline protective effect was not considered worth keeping. In order to assess the associations with occupational exposures, we included all the expert-based quantitative phase-2 exposure scores (asbestos, man-made mineral fibers, PAH, crystalline silica, mild steel welding fumes, stainless steel welding fumes, iron mining, painting, strong acids, and DME) and performed a backward selection procedure, keeping all the exposure variables with a P-value for inclusion of <10%. For the quantitative exposure variables thus selected, we then fitted a model including the indicator variables of the exposure tertiles compared to the non-exposed in order to check for non-monotonous patterns. Quartiles as used in the previous paper (10) led to a non-identifiable model.
Simulations
In order to document the added power due to the 2PCC design as compared to the standard analysis of a random subsample, we sampled 1000 times the phase-2 exposure for all subjects not belonging to phase 2: separately for cases and controls, we assigned the expert-assessed exposure of a phase-2 subject randomly chosen from the same stratum to each subject not in phase 2.
Firstly, from each such completed phase-1 dataset, we randomly drew 215 cases, and 269 controls were analyzed using standard logistic regression for comparison with the results in table 3.
Table 3
Results of the multiple two-phase logistic models [AF=attributable fractions in %; DME=diesel motor exhaust; OR=odds ratio; PAH=polycyclic aromatic hydrocarbons; 95%CI=95% confidence interval;]
Secondly, in order to document the power of the 2PCC design with less subjects in phase 2, we sampled 1000 times five cases and controls (or all subjects if <5 had been subjected to an expertise) from each stratum of phase 2, that is 105 controls and 100 cases, and analyzed them using 2P logistic regression.
In parallel, we randomly sampled – without 2P stratification – 105 controls and 100 cases from each of the 1000 completed datasets described earlier and analyzed them using standard logistic regression.
All analyses used the same list of independent variables for the analysis of the three series of simulations as outlined in table 3. This list comprised the confounders and the four quantitative occupational exposure scores.
Results
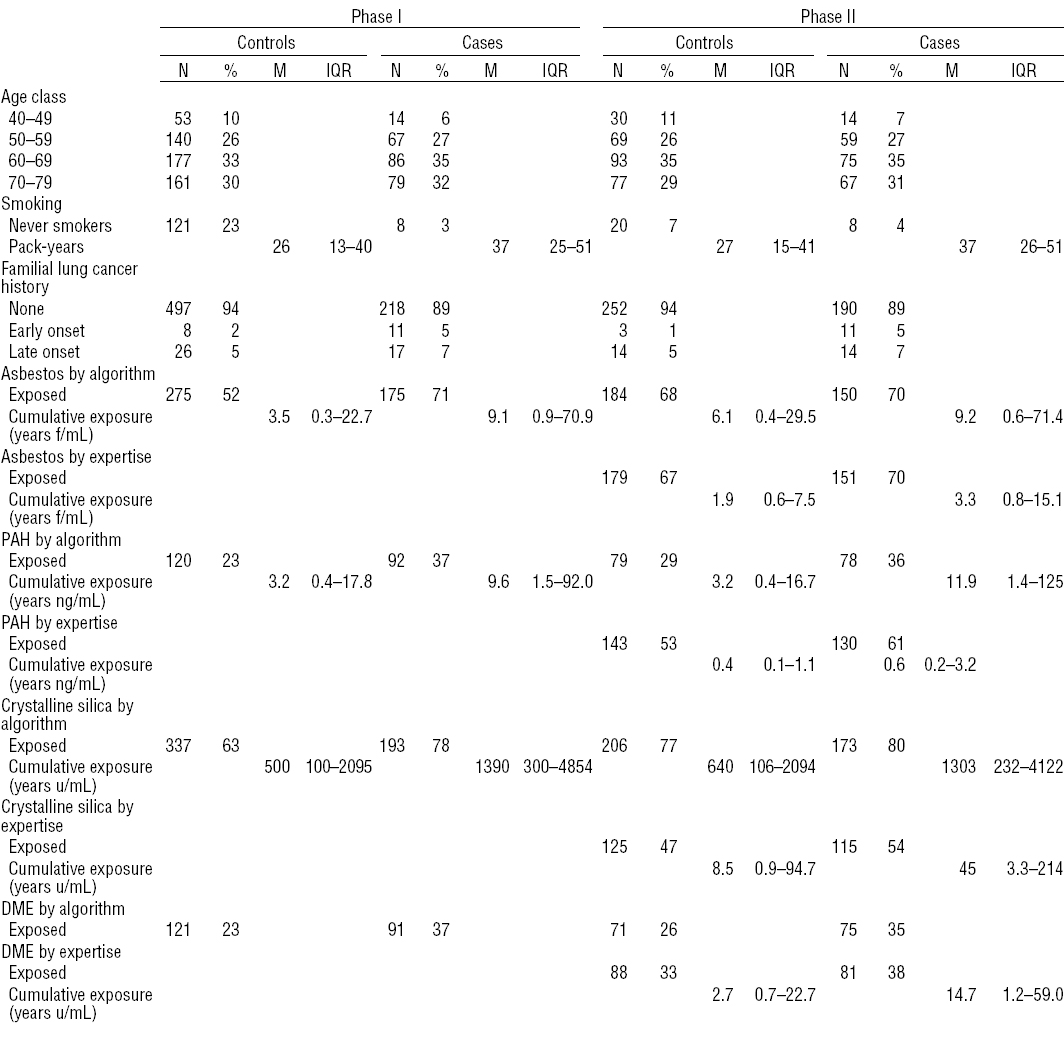
Table 2 shows that the age-structure of cases and controls in our original data was similar in phases 1 and 2. On the other hand, the number of smokers and the number of exposed subjects was by design overrepresented in phase-2 controls. Among cases there were few differences between phases 1 and 2. A second striking feature is that the experts identified more subjects exposed to PAH and much fewer for silica than the algorithm. However, in the phase-2 dataset, the algorithm-based exposure indices were all higher than the corresponding expert-based estimates.
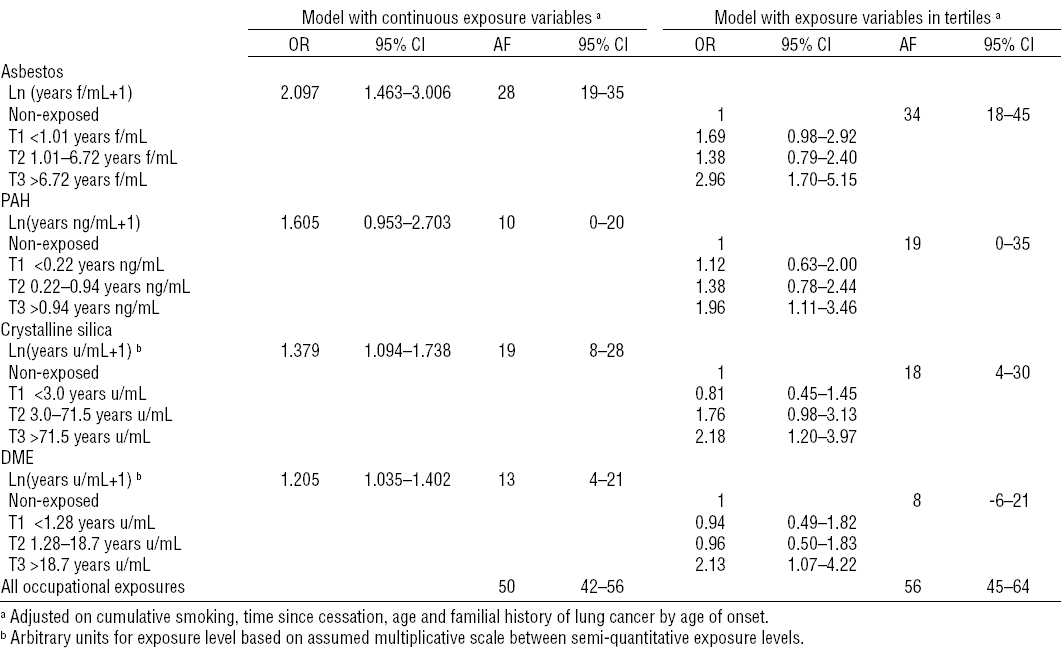
Table 3 provides the results of the 2-phase analysis. When running the backwards selection procedure, only asbestos, PAH, crystalline silica, and DME remained in the model (data not shown). Statistically significant dose–response slopes were observed for asbestos, crystalline silica, and DME and borderline for PAH adjusting for quantitative smoking and time since cessation, age, and familial history of lung cancer by age of onset.
Moreover, all the odds ratio (OR) corresponding to the highest exposure tertiles were statistically significant and all either >2 (asbestos, silica and DME) or very nearly so (PAH).
The estimated fractions attributable to occupational exposure were high (>50% for all the selected occupational carcinogens) but of same order of magnitude than in the analysis of the full phase-1 data using algorithmic exposure scores given in Wild et al (10): 56% (41–67%) for continuous scores, 52% (32–66%) for discretized scores.
The simulations of the 1000 unstratified random subsets of the same size as our phase-2 study, led to statistical significance in 100% of the cases for asbestos, but only 39% for silica, 13% for PAH and 20% for DME. This should be interpreted bearing in mind the P-values in our 2PCC analysis presented in table 3 (asbestos 0.0001, silica 0.009, PAH 0.08, DME 0.02). Concerning the simulation study of the smaller samples of 105 controls and 100 cases, the number of statistically significant results from the subsets of the 2PCC, respectively for the simple random samples again without the 2-phase-specific stratification, were 85% versus 70% for asbestos, 26% versus 20% for silica, 19% versus 10% for PAH, and 62% versus 11% for DME. One can note that for DME, the 2PCC sample of 205, was more often significant than the unstandardized random sample of 484. The results from these simulations document the added power of the 2PCC design.
Discussion
In this paper, we showed the power of the 2-phase study design. Despite a limited sample size, a statistically significant dose–response relationships could be identified for asbestos, PAH, crystalline silica, and DME simultaneously when using expert-based exposure assessments in such a design. This efficiency gain is further substantiated by the comparison of simulations of unstratified random subsets of cases and controls with 2PCC studies of the same size. Moreover, we devised maximum-likelihood estimates and confidence intervals of attributable fractions within 2PCC studies which were as yet unavailable.
First, we discuss the specifics of the 2-phase design. This design is based on a stratification on an exposure estimate that is available before any expert assessment. In the case of our study, we used an algorithmic exposure assessment but a job-exposure matrix (JEM) could have been an alternative source for such phase-1 exposure estimate. A striking feature of the phase-2 dataset is its design-based difference with the total sample. As shown in table 2, 68% of the phase-2 controls were found to be exposed to asbestos compared to 52% of phase-1 controls. This biased selection, which is, moreover, different between cases and controls, might seem counterintuitive to epidemiologists. However, this is completely taken into account by the weighting performed in the dedicated statistical analyses for which packages in SAS (14) as well as in R (17) are now available. These weights do not only correct for this lack of representativeness but also add some information from phase 1, ie, some power. This added information is more important if the stratification is finer, but for statistical reasons, the strata must not be too small. This led to our choice of the median exposure as the cut-point between categories and our decision to collapse some strata resulting from the cross-classification of the phase-1 exposure variables.
What did we gain with respect to a full assessment? In the present study, we included 484 subjects in the second phase for expert assessment out of 777 study participants; thus, while saving nearly 300 expert assessments, the effort was still substantial. However for the simultaneous detection of the four dose–response relationships, the number of subjects included in phase 2 seems adequate as this showed quite clear-cut associations for the most frequent occupational carcinogens. When comparing with the simulations of a random subsample of the same size, it becomes clear that the chance of having such simultaneous associations would have been highly unlikely, again documenting the gain in power through the 2PCC design.
It must however be stressed that the full benefit of 2-phase studies is more apparent when the exposure prevalence is low. In such a case, a random sample of cases and controls would include too small a number of exposed study participants to lead to any clear dose–response relationship. The power of 2PCC studies is mostly driven by the size of the phase-2 sample and the exposure distribution therein, although as mentioned before, phase 1 contributes some information. The size of phase 2 would thus not have to be increased in the case of a phase 1 with several thousand cases and controls in a low-exposure prevalence area. This assumes however that the phase-1 exposure assessment methods, and hence the stratification, identify the exposed subjects with sufficient accuracy. If the phase-1 stratification is less efficient in identifying these rare exposures, the result will be a reduction of the overall efficiency of the 2-phase design.
As an example, one could consider a study focused on the carcinogenic potential of man-made mineral fibers (MMMF) in the absence of asbestos – a rare occurrence, see for example (18) – it would be possible to apply a stratification on an algorithmic exposure or a JEM cross-classifying asbestos and MMMF. The 2PCC study would include all cases and controls instead of a random sample, for which phase 1 would suggest an MMMF exposure without asbestos. The expert assessment in phase 2 would then confirm this pattern of exposure (or not) and have greater power in detecting any specific association with MMMF.
Next, we discuss the use of experts. First, while we acknowledge that no expertise can be perfect, the data collection was, to our knowledge, reasonable in the context of a retrospective study and allowed for as-good-as-possible evaluation. When considering continuous cumulative exposure variables, we observed much higher dose–response slopes than in our previous paper, although when considering the categorical classes, the OR are quite similar. This is partly due to the fact that the cumulative exposure indices were systematically larger when assessed by the algorithms compared to the expert-based indices. This might indicate that the algorithmic scores associated with some tasks were tuned to the worst cases whereas the expert estimation could be more differentiated in assessing lower exposure when warranted. However, in order to explore whether this might also be due to exposure misclassifications, we divided the individual algorithmic cumulative exposure scores (not log transformed) by a single constant so that the mean (log-transformed) algorithmic and expert-based cumulative exposure scores were approximately equal. The aim of this transformation was to try to homogenize the units between the two exposure assessments in order to be able to compare the slopes. For asbestos as well as for PAH and crystalline silica (data not shown), the expert-based dose–response slopes were still steeper than those based on the algorithmic exposure estimates. As the units are now assumed to be the same, this tentatively supports the use of expert-based exposure assessments as compared to our algorithmic scores. This is in contrast to recent results (19, 20) showing that, if based on closed form questions, algorithmic exposure estimates perform as well as expert assessments. In that case, the more transparent and reproducible algorithmic assessment should be preferred. On the other hand, when not sufficiently detailed closed form questions are available or when it is necessary to interpret open questions, as was the case for DME exposure in our study, an expert assessment is the only achievable way to obtain quantitative exposure estimates.
Finally we discuss the substantive aspects of the present paper. Our expert exposure assessment confirmed the dose–response relationships based on algorithmic exposure estimations that we had observed in an earlier analysis of the algorithmic part of this case–control study for asbestos, crystalline silica and, partially, for PAH (10). What is new is the significant dose–response for DME based on the individual expert assessments. This is in agreement with the recent classification of the IARC of diesel as a group 1 carcinogen, but we know of no population case–control study having shown such a dose–response relationship. It is to be noted that the test for the dose–response somewhat arbitrarily relies on the linear fit of the log-transformed scores. This trend roughly fits the presented analysis by tertiles if one allows for the large confidence intervals in the OR estimation. There is however a hint at a possible non-linearity for DME, as there is no excess risk in the two lowest exposure tertiles.
These results must be interpreted bearing in mind the overall strengths and weaknesses of the case–control study discussed extensively in our previous paper (10). Briefly, the results of this paper show a prevalence of occupational exposure in the study area, which is higher than in most published papers. This high exposure prevalence might be partly due to methodological differences with other studies in the exposure assessment, but the fact that the overall lung cancer and mesothelioma rates in the study area are very high is consistent with the present findings. The controls were selected based on a random digit dialing procedure. Although this may have led to selection bias, this is unlikely as the same procedure was applied to the cases who were not interviewed if they could not be reached by telephone.