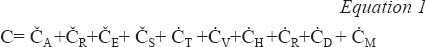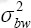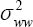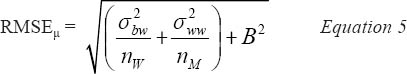A suitable exposure assessment is central to occupational health research, not the least as guided by the need to obtain data assuring that statistical power is sufficient to render the study informative. Power in studies comparing exposures between groups or conditions within groups is directly dependent on the precision of the mean exposure estimate, as exemplified by studies of biomechanical exposure (physical workload) (1, 2). This precision, in turn, depends on the sample size, and the variability in exposure caused by differences in behavior between subjects and within subjects across time, as well as by uncertainty associated with the exposure measurement method per se (3, 4). Exposure variability, often expressed in terms of exposure variance components, has been an issue in occupational epidemiology for more than two decades (5–7), with applications reaching far beyond the design of data collection strategies (8). In the field of biomechanical exposures, to which the present paper is specifically devoted, exposure variability was introduced in the mid-1990s (9–11), and a number of papers have discussed exposure assessment strategies, including necessary sample sizes to ensure a certain precision of a mean exposure estimate and/or a sufficient power in comparison studies (1, 3, 12–17). Although these articles have furthered inquiry into efficient exposure assessment from a statistical point of view, they have been criticized for rarely acknowledging the actual costs of exposure assessment. Thus, a 2010 systematic review of literature focusing on cost-efficient collection of exposure data (18) found only nine studies dealing with the trade-off between statistical performance and monetary resources invested in obtaining that performance, even if some studies have appeared after 2010 (19–21). Only some of the publications identified in the 2010 review dealt specifically with occupational or environmental exposures (7, 22–26); only two of these included empirical data to illustrate cost and efficiency (24, 26), and none were devoted to assessment of biomechanical exposure. In the context of study design, the trade-off between cost and statistical performance appears in the form of either one of two questions: (i) for a given research budget, which measurement method and sampling strategy delivers the highest statistical performance with respect to producing unbiased and precise data? and (ii) facing a required statistical performance, for instance in order to obtain sufficient power, which method and sampling strategy is the most cost efficient?
Biomechanical exposure assessment methods are often grouped into three broad categories or “classes” of measurement: direct measurement, observation on-site or from video, and worker self-report. Objective direct measurement methods are generally preferred for accuracy (27–31). Observation has long been believed to represent a middle ground in that they are more objective than self-reports (19, 27, 29), yet less consistent than direct measurements. The suspected inferior precision associated with using observational methods would mainly be a result of variability introduced by within- and between-observer differences in opinions when viewing the same posture (21, 32–34). At the same time, observations have been anecdotally claimed to be cheaper in use than direct measurements (27). This would mean that, for a certain budget, more data could be collected by observation, which might make up for the larger exposure variability, and eventually lead to a more precise estimate of group mean exposure than that obtained by direct measurements at the same total cost. In order to appreciate this trade-off and decide which measurement method to prefer from a cost-efficiency point of view, costs and efficiency must be quantified for each measurement class under realistic data collection scenarios and then compared (18). However, there have been few comprehensive efforts to report the empirical costs of biomechanical exposure assessment, and these preliminary efforts did not include any information on the quality or statistical properties of exposure information delivered (35–37). Recently some studies have combined empirical costs and precision of occupational exposure estimates, although these have addressed cost efficiency in general terms (20), or have focused on a narrow assessment of cost and compared sampling or analysis strategies just within a single method [in casu, observation; (19, 21)].
In this study, empirically collected cost and exposure data were used to assess the cost efficiency of two common classes of methods for assessing working postures: direct measurement by inclinometry using data loggers and video-based posture observation by trained analysts. The objectives were to: (i) quantify and compare the trade-off between costs and statistical performance (ie, cost efficiency) when using inclinometry and observation to retrieve mean exposures to trunk and arm inclination variables in groups; and (ii) identify possible changes to the relative cost efficiency of the two methods when different alternative study design scenarios are considered.
Methods
Study population and sampling
Twenty-seven randomly selected full- or part-time baggage handlers at a large Swedish airport had their trunk and upper-arm postures assessed during three work shifts each using three methods: self-report via questionnaire, observation from video film, and full-shift inclinometer registration using tri-axial accelerometers (only the observation and inclinometer data were included in this paper). Video recordings and inclinometer measurements were made in parallel, and therefore represent the same period of work for each specific subject. All subjects signed an informed consent form and the Regional Ethical Review Board in Uppsala, Sweden, approved the study. Measurements were successfully collected for 3 days from all but one worker who could not complete a third day due to injury, resulting in measurement files from 80 days in total. Data were successfully processed for all these files, except for one inclinometer file which had excessive noise. The data collection methods are described in detail in a separate report (35), as are the data processing methods (37).
Inclinometer data collection and processing
Trunk and upper-arm posture was assessed as inclination with respect to the line of gravity. An inclinometer with an integrated memory (VitaMove triaxial accelerometer system, 2M Engineering, Veldhoven, the Netherlands) was placed on each upper arm over the medial deltoid, and on the trunk between the shoulder blades. Inclinometers were set up before the start of the shift, worn for the duration of the shift, and data were downloaded to a laptop computer at the end of the shift. Inclinometer data were calibrated to each subject’s recorded “zero” positions. For the upper arms, the zero position was to bend forward and hold a 5 kg weight in the hand. The trunk’s reference positions involved bending forward (to define “forward”) and then standing upright (to define zero) as described in Teschke et al (38). The raw three-axial data from the inclinometers were calibrated and transformed into degrees by using the same software used by Wahlström et al (39) and Hansson et al (28). In this software, a 5 Hz low-pass filter is used to reject inclination errors due to rapid movements. This software has been validated when used together with a similar type of accelerometer (40, 41). Inclinometer data were also processed to account for extreme trunk and upper-arm angles when workers were resting supine. Data from each measurement day were summarized into daily inclination metrics for both the trunk and each arm: median as a measure of central tendency, 90th percentile as a measure of extreme values, and the percent time spent with flexion (trunk) or elevation (upper arm) >60° as a measure of the occurrence of clearly non-neutral postures. This is consistent with metrics commonly used in other inclinometer studies (39, 42, 43). Since mean exposure values and components of variance were very similar for the left and right arm, only the right arm is presented for the sake of simplicity.
Observation data collection and processing
Workers were video recorded using a single camera following them throughout the airport during their regular work tasks for the first or second half of their work shifts. Video recordings were analyzed by four trained observers using a customized software program similar to that described by Bao et al (44, 45). Software users operated a point-and-click dial to estimate each posture at a 1° resolution with respect to gravity in each still frame. Bao et al (45) has reported the between-rater standard deviation (SD) using a 1° resolution method to be 5.5° for the trunk and 10.8–12.6° for the upper arm. Still frames were selected at 55-second intervals, yielding up to 252 unique frames per the half-shift. Trunk and upper-arm inclination were summarized into the same daily exposure metrics as those selected for the inclinometer (ie, median, 90th percentile, and percent time with the upper arm elevated >60°).
Measurement costs
Comprehensive costs for data collection and processing were tracked throughout these phases and used to developed cost models; these methods have been reported in detail elsewhere (35, 37). In brief, the time for all research staff was recorded and summarized for all major research tasks for both measurement methods, from study planning to worksite measurements to data management. The comprehensive cost, C, combining data collection and processing costs for each method, can be assessed using the following model (fixed costs are denoted by Č and variable costs denoted by Ċ):
Where ČA is the cost of project meetings and administration including documentation, budgeting, and internal correspondence; ČR is cost related to recruitment, including corresponding with employer and scheduling; ČE is the capital cost for data collection equipment; ČS is the cost for developing customized data processing software. In terms of variable costs, ĊT is the cost of training staff to collect and process data specific to the measurement method; ĊV is the cost of traveling to the worksite for data collection (depending on the number of trips), ĊH is the cost of hotel accommodations during overnight trips (depending on the number of nights); ĊR is the cost of recruiting workers at the worksite (depending on unit cost of recruiting a worker, ċR, and the number of workers recruited); ĊD is the cost of onsite data acquisition (depending on the unit cost of a measurement day, ċD, and the number of data collection days); and ĊM is the cost of managing the processing of daily data files (depending on the unit cost of processing a data file, ċF, and the number of data collection days). Equation 1 is an amalgamation of previously-published cost models for data collection (35) and data processing (37). All costs were converted from Swedish kronor to euros using average annual exchange rate for the calendar years data were collected or processed.
Estimating statistical performance
In this study, the statistical performance of a measurement class was measured in two ways: as the precision of the obtained group mean exposure estimate, including only random error sources, and as the root-mean-squared error (RMSE) of the estimate, including both bias and random error of the estimate. Exposure variance components were estimated according to the following model:
where:
-
xij is the exposure for worker i on day j;
-
μ is the overall group mean value for a given exposure metric (ie, median, 90th percentile, % time >60°);
-
α1 is the random effect of worker i (values of i from 1–27); and
-
εij is the residual error representing the random effect of measurement day j (values of j from 1–3) in worker i.
A similar model has been used to estimate posture variance components in previous studies (39, 46). Based on this model, variance components were estimated using Restricted Maximum Likelihood (REML) via the VARCOMP command in SPSS version 20.0 (IBM, Armonk, NY, USA) with “worker” as a random effect term. The random effect terms αi and εij are then presumed to have a mean of 0 and variances of (between-worker variance) and (within-worker variance), respectively. In the case of our observations, these variances include a non-extractable contribution from within- and between-observer rating variability.
Precision
The variance of the estimated mean, 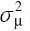 , for an exposure metric is:
, for an exposure metric is:
where:
For descriptive purposes, precision may be expressed in terms of the standard error of the mean (ie, 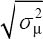 )
)
and statistical performance
– only including random error – conveniently as the inverse of this standard error (ie, 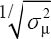 ) (19).
) (19).
Precision and bias combined
Statistical performance was also quantified using the RMSE of the group mean exposure estimates. RMSE includes both random
variance of the estimated mean of the exposure metric 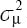 , and the possible systematic bias inherent in the chosen method, B, such that:
, and the possible systematic bias inherent in the chosen method, B, such that:
Substituting Equation 3 into Equation Equation 4 expresses the combined effect of bias and (im)precision:
To be consistent with previous literature describing the hierarchy of exposure assessment methods (27), inclinometry was designated as the method producing “correct” inclination data. Thus, by definition, the results obtained
by inclinometry were taken to be unbiased (B=0), and the bias, B, of the results obtained by observation was calculated as
the difference between mean exposures obtained by observation and the corresponding results according to inclinometry. The
combined precision and bias performance of each posture assessment method was calculated as the inverse of the RMSEμ (19, 21), which is thus, by definition, equal to 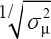 for inclinometry in the present case.
for inclinometry in the present case.
Quantifying cost efficiency
The “price for performance” was expressed in euros per 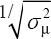 and 1/RMSEμ (ie.
and 1/RMSEμ (ie. 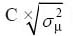 and C × RMSEμ) for the precision-only and combined performance measures, respectively. These metrics for quantifying cost efficiency were
selected for conceptual convenience, since an increased value will reflect an increased cost relative to the precision delivered.
Thus, the most cost-efficient option among compared alternatives can be identified as the one with the smallest value for
this metric.
and C × RMSEμ) for the precision-only and combined performance measures, respectively. These metrics for quantifying cost efficiency were
selected for conceptual convenience, since an increased value will reflect an increased cost relative to the precision delivered.
Thus, the most cost-efficient option among compared alternatives can be identified as the one with the smallest value for
this metric.
Exploring cost efficiency under alternative study conditions
The cost-efficiency analysis procedure presented here can be used as a study planning tool to compare different research settings and conditions. As an illustration, effects on total study cost and statistical performance were investigated for three different scenarios: (i) the case of the current study, where researchers started from scratch by developing new methods, conducting all data collection, and processing; (ii) immediate duplication, where the data must be collected but equipment, protocols, trained staff and processing methods already exist; as would be encountered if data from an additional population of flight baggage handlers at another airport with similar logistics were collected again immediately; and (iii) inheriting data from another researcher, where the data are already collected and only need to be processed. Scenario 2 differs from the current scenario by removing costs for equipment (ČE), software (ČS) and training (ČT) in the calculation of total cost (equation 1). Scenario 3 removes all the fixed and variable costs associated with data collection, limiting costs to those associated with data processing (see table 1).
Table 1
Cost components (cf equation 1) in euros for the mea-surement methods and exposure data sample in the current study.
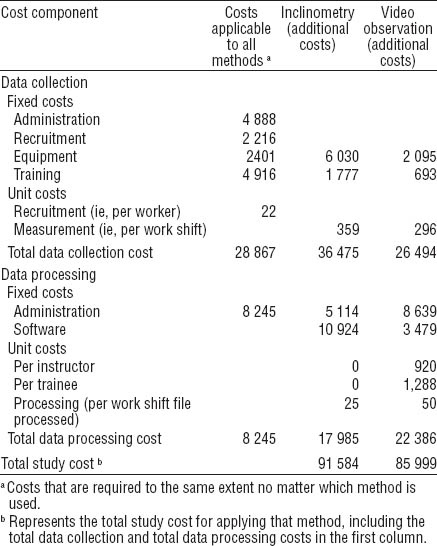
Since the relative impact of fixed and variable costs differs with the sampling strategy, the referable method in terms of cost efficiency may differ between studies of different sizes. To investigate this, the current study and the two alternative scenarios were explored further with simulated sample sizes. Thus, for samples ranging from 5–50 participants with three measurement days each (15–150 measurements in total), the comprehensive (fixed and variable) cost was determined [cf equation (1)], together with statistical performance [cf equations (3) and (4)], using the variance components and bias from the current study.
Results
The data collection, data processing, and combined costs for both classes of measurement are reported in table 1; the descriptive statistics, bias, and variance components for each exposure metric are reported in table 2.
Table 2
Descriptive statistics for the two body parts, the two measurement methods, and the three posture variables in the current
study. [Mean=group mean across all measured shifts; bias=deviation of the mean group exposure from the value obtained using
inclinometry; nW=number of workers; nM=number of mea-surements; sBW=between-worker standard deviation; sWW= within-worker
standard deviation; 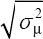 =standard error of the mean; RMSEμ=root mean squared error of the mean].
=standard error of the mean; RMSEμ=root mean squared error of the mean].
Simulated sampling strategies for the trunk and right arm are depicted for all three exposure metrics in the current scenario
(figure 1), the case of immediate study duplication (figure 2), and the case of inherited data (figure 3). The ten individual points on each curve illustrate study designs including 3 measurements on each of 5–50 workers, increasing
in increments of 5. These figures demonstrate the statistical performance of the methods in terms of inverse standard error
(precision) of the mean (ie, 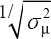 ) or in terms of inverse RMSE (combined precision and bias, ie, 1/RMSEμ). An increase on the y-axis therefore means an increase in statistical performance. Statistical performance is shown relative
to the total study cost in kilo-euros (x-axis); as the number of workers increases from 5 to 50 and the number of measurements
from 15 to 150, the total study cost but also performance increases. For example, figure 1a shows precision of median trunk and arm angle as measured by both inclinometer and video observation for a variety of study
designs ranging in cost from €50 000–140 000. At the left-most points on the graph with only 15 measurements (5 subjects for
3 days), most of the costs identified for each method are fixed, due to the initial investment in equipment, planning, and
training necessary to allow any measurements in the case where all planning, data collection, and data processing must be
performed by the researchers (cf. table 1). For the most minimal study depicted in figure 1a costing roughly €50 000, the performance (
) or in terms of inverse RMSE (combined precision and bias, ie, 1/RMSEμ). An increase on the y-axis therefore means an increase in statistical performance. Statistical performance is shown relative
to the total study cost in kilo-euros (x-axis); as the number of workers increases from 5 to 50 and the number of measurements
from 15 to 150, the total study cost but also performance increases. For example, figure 1a shows precision of median trunk and arm angle as measured by both inclinometer and video observation for a variety of study
designs ranging in cost from €50 000–140 000. At the left-most points on the graph with only 15 measurements (5 subjects for
3 days), most of the costs identified for each method are fixed, due to the initial investment in equipment, planning, and
training necessary to allow any measurements in the case where all planning, data collection, and data processing must be
performed by the researchers (cf. table 1). For the most minimal study depicted in figure 1a costing roughly €50 000, the performance (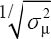 ) for trunk observation data (black squares) of ~0.41 on the y axis corresponds to a standard error of the mean of approximately
2.43° (1/0.41). Statistical performance increases steeply with an increase in investment towards the right-hand side of the
graph, resulting in a value of roughly 1.30 (ie, a standard error of the mean of approximately 0.77°) at the study including
50 subjects, which costs €140 000.
) for trunk observation data (black squares) of ~0.41 on the y axis corresponds to a standard error of the mean of approximately
2.43° (1/0.41). Statistical performance increases steeply with an increase in investment towards the right-hand side of the
graph, resulting in a value of roughly 1.30 (ie, a standard error of the mean of approximately 0.77°) at the study including
50 subjects, which costs €140 000.
Figure 1
Statistical performance in terms of precision only (a, c, e), and combined precision and bias (b, d, f) by study cost for trunk and right arm inclination across the three investigated posture variables for the current study design. Closed triangles (▴) represent trunk inclinometry; open triangles (△) represent trunk observation; Closed squares (◼) represent arm inclinometry; open squares (◻) represent arm observation. Solid and dashed vertical lines indicate the cost of the current study for inclinometry and observation, respectively.
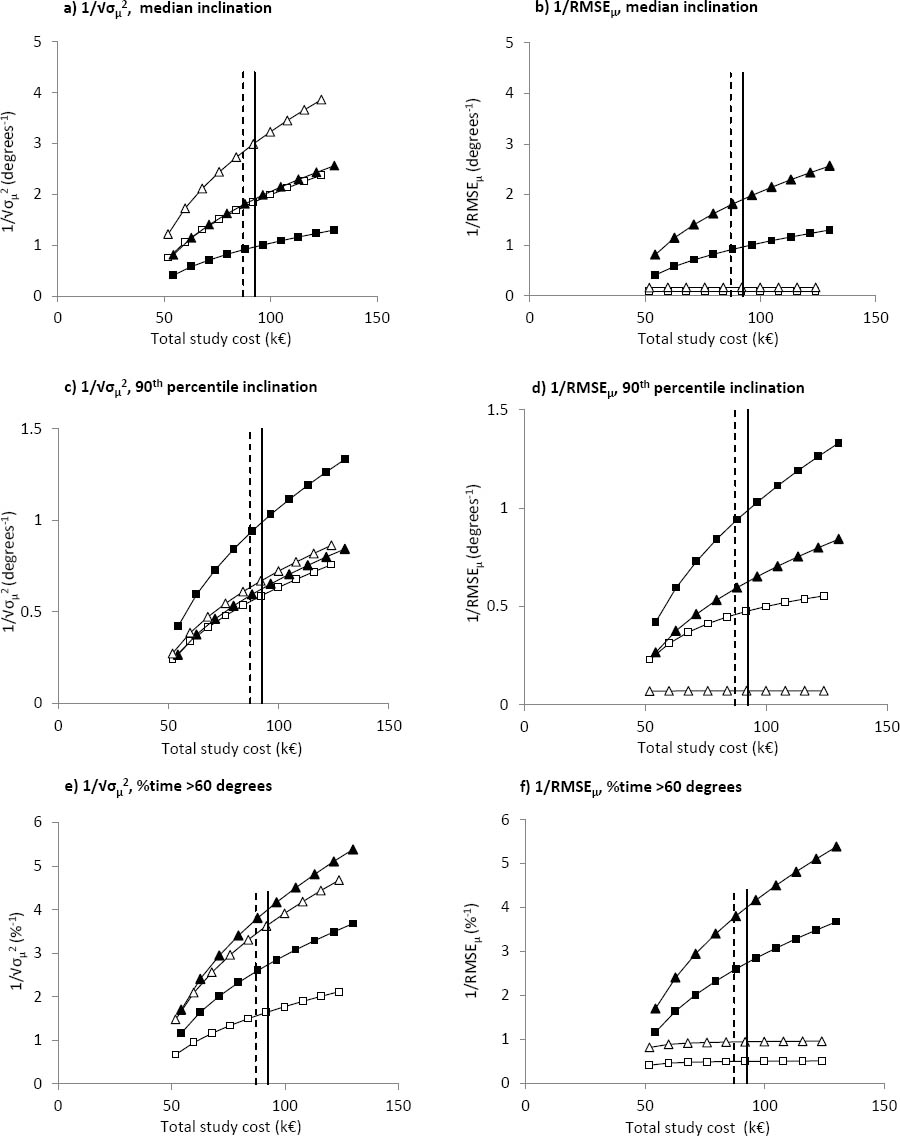
Figure 2
Statistical performance in terms of precision only (a, c, e), and combined precision and bias (b, d, f) by study cost for trunk and right arm inclination across the three investigated posture variables for the case of immediate study duplication. Closed triangles (▴) represent trunk inclinometry; open triangles (△) represent trunk observation; Closed squares (◼) represent arm inclinometry; open squares (◻) represent arm observation.
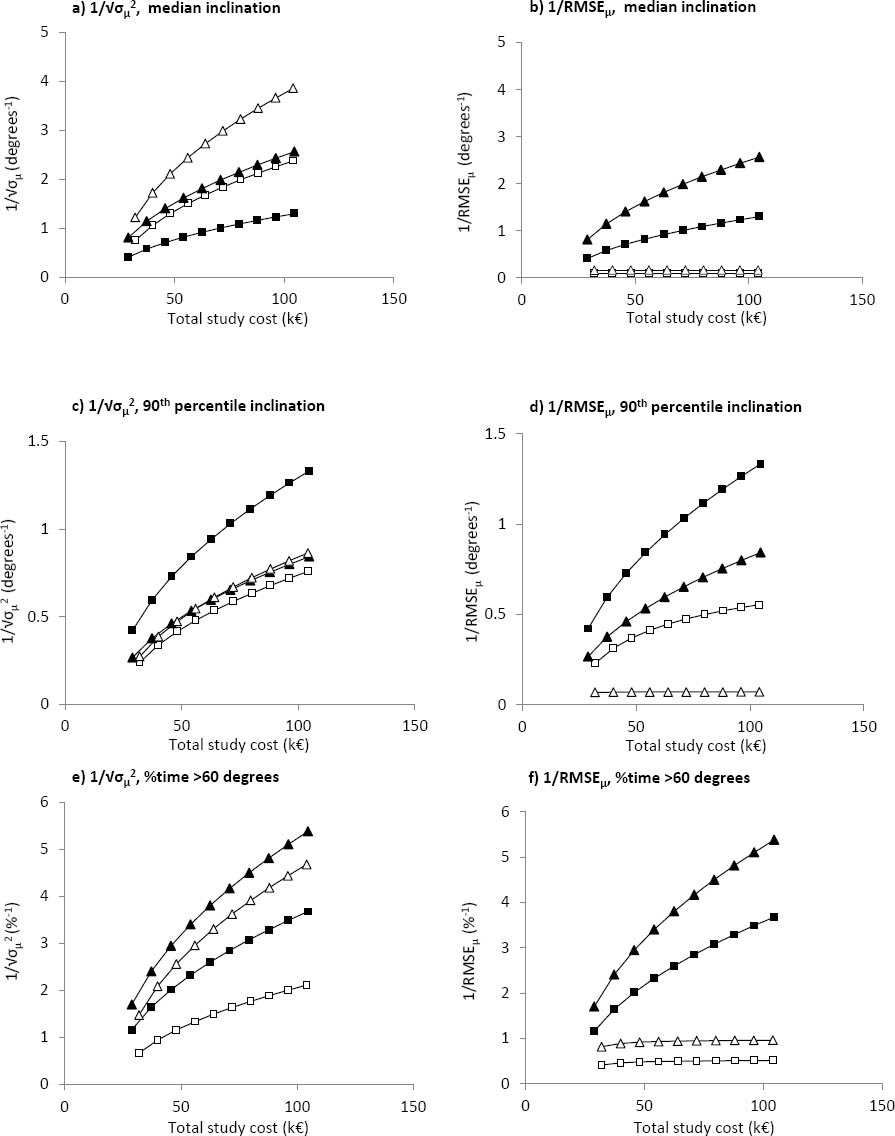
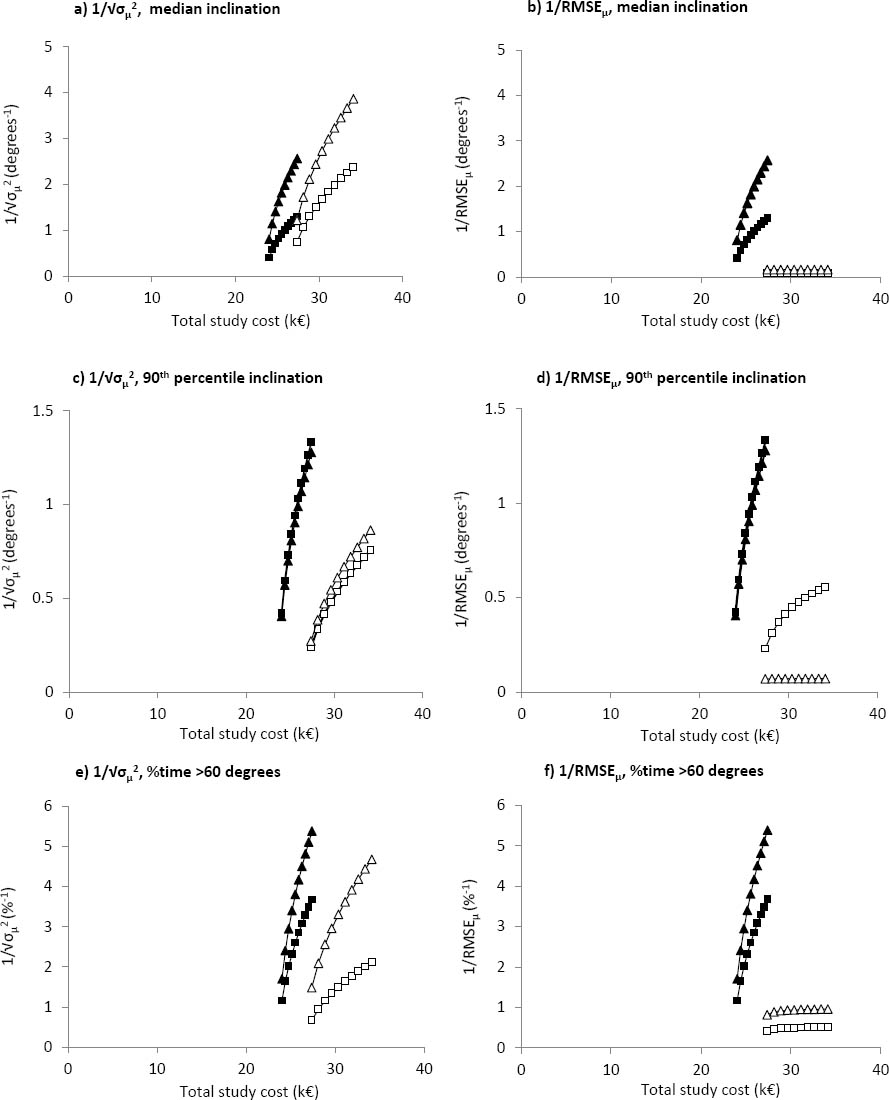
Figure 3
Statistical performance in terms of precision only (a, c, e), and combined precision and bias (b, d, f) by study cost for trunk and right arm inclination across the three investigated posture variables for the case of inherited data. Closed triangles (▴) represent trunk inclinometry; open triangles (△) represent trunk observation; Closed squares (◼) represent arm inclinometry; open squares (◻) represent arm observation. Note that the scale on the x-axis differ from that in figures 1 and 2.
Scenario 2 (figure 2) has intermediate fixed costs, since the costs of equipment and training for both data collection and processing are assumed
to be zero. For example, figure 2a also shows trunk observation to have the best statistical performance in terms of precision,
but the same levels of performance (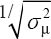 of 0.41 and 1.30) which entailed prices of €50 000 and €140 000 in scenario 1 can now be obtained for a lower study cost:
€32 000 and €104 000, respectively.
of 0.41 and 1.30) which entailed prices of €50 000 and €140 000 in scenario 1 can now be obtained for a lower study cost:
€32 000 and €104 000, respectively.
Scenario 3 (figure 3) eliminates all the costs of data collection, but the fixed costs for software development, training, and administration costs are still over €20 000; this fixed cost comprises the bulk of the study cost on the left-most data point with only 15 measurements. Moving towards the right-hand side of the graph, total study costs increase as determined by the unit cost of additional measurements to a maximum of €33 000 with 150 measurements.
Discussion
Comparing inclinometer and observation: the effect of bias and precision
For both median arm and trunk inclination, observation demonstrated better precision when estimating the group mean exposure
(ie, smaller 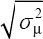 , table 2), while inclinometry was more precise for the other two arm inclination variables. For trunk 90th inclination percentile and % time inclined >60°, the two methods had almost the same precision (table 2). When costs were also considered and precision alone was used as the indicator of statistical performance, observation still
delivered the best performance (ie, the largest
, table 2), while inclinometry was more precise for the other two arm inclination variables. For trunk 90th inclination percentile and % time inclined >60°, the two methods had almost the same precision (table 2). When costs were also considered and precision alone was used as the indicator of statistical performance, observation still
delivered the best performance (ie, the largest 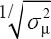 ) for median inclinations at any particular cost (figure 1a), while inclinometry was more cost-efficient for the % time >60° (figure 1e). For 90th percentiles, inclinometry was more cost-efficient for the arm but less cost-efficient for the trunk (figure 1c). The cost-efficiency relationship between inclinometry and observation was maintained at all simulated sample sizes (figures
1a,,1c,1e), indicating that the optimal method was consistent over the investigated range of sample sizes.
) for median inclinations at any particular cost (figure 1a), while inclinometry was more cost-efficient for the % time >60° (figure 1e). For 90th percentiles, inclinometry was more cost-efficient for the arm but less cost-efficient for the trunk (figure 1c). The cost-efficiency relationship between inclinometry and observation was maintained at all simulated sample sizes (figures
1a,,1c,1e), indicating that the optimal method was consistent over the investigated range of sample sizes.
For several observed metrics, between-worker variability was estimated to be zero (table 2), which is one reason that observations performed well in terms of precision (equation 3). “Zero” between-worker components of variance have been reported previously in observation studies of lumbar posture (47), and they may be an artifact associated with the algorithms used for distributing the overall variance in data between different sources. Thus, if within-worker variability is very large, little or no variability will be “left” for the between-worker component, especially if this component is, truly, small (48). In our study, observer variability may have contributed to inflating within-worker variability, as indicated by most of these variabilities being larger in observed data than in the corresponding inclinometer measurements (table 2).
However, when bias was also considered, the performance of inclinometry relative to observations improved substantially, since the inclinometers were considered to give correct data. The bias associated with observations was substantially higher than the random exposure variability for the body parts and exposure metrics studied, resulting in greater cost efficiency for inclinometry (figures 1b,1d,1f). The advantage of inclinometry was maintained across all investigated sample sizes. This result clearly illustrates the importance of recognizing possible bias when documenting the statistical performance of different measurement methods. This is rarely done in occupational epidemiology, probably because the extent of bias is unknown, especially in studies addressing only one exposure assessment method. The status of inclinometry as “best performer” in the present case is due entirely to the a priori decision to designate inclinometers as giving “correct” data, which is standard in occupational studies (38, 49, 50). If observations were designated as the method producing correct results from which to calculate bias, the observation method would have had better relative performance than inclinometers when bias and precision were combined. If both observations and inclinometer results were, in fact, biased compared to some unambiguous but (as of today) unknown gold standard for posture measurement, their rank in terms of cost efficiency would remain as found here if both were either negatively or positively biased, while the relationship might change if their biases had different signs (ie, if the gold standard result were somewhere in-between the results obtained by inclinometry and observation). In the absence of an unambiguous gold standard, the decision to identify inclinometers as producing correct results is consistent with established thinking regarding the hierarchy of method classes in biomechanical exposure assessment (27, 29). The result that observation appears to estimate the group mean of median inclination with greater precision than inclinometers is, however, novel.
Video observation consistently underestimated postures compared to inclinometer measures for all metrics and body parts (table 2). This is opposite to what has been reported in a study of hairdressers’ upper-arm postures, where video observers overestimated inclination angles (21). A lab-based study identified an observation over-estimation in higher exposure ranges for trunk flexion when compared to opto-electric tracking (51); validation studies of neck flexion also showed observations to over-estimate when compared to an inclinometer (52). Lab tests rarely imitate the exposure distributions seen in occupational studies, since experiments generally favor a balanced design with equal proportions of measurement throughout the exposure range. Real work exposure is more likely to be skewed with fewer high exposure instances. In a comparison of field-based observation and inclinometry of trunk postures during real work, Village et al (33) showed that observation underestimated the proportion of time spent in trunk extension, in lateral bending, and in 20-45° of flexion (the most frequent non-neutral category), while over-estimating the time spent in neutral postures. It may be that the sampling rate of both the Village et al study and the current observation design are not adequate to capture the relatively less frequent extreme postures. In this vein, a study of the effect of sampling size on bias and precision of estimates of upper-arm elevation obtained using inclinometers showed that 90th percentile inclinations were underestimated when samples were short, and thus less likely to capture rare, extreme posture events (53). If the same effect were also found for work sampling at low frequencies, one would expect the current study’s results to show more bias for the 90th percentile than the median, but this was, in fact, only the case for trunk inclination.
It should also be noted that the observations were based on a single-camera image. This may introduce error since a three dimensional phenomenon is being represented by a two-dimensional image. It is ideal to have a perpendicular view of the trunk to assess flexion/extension of the trunk flexion and upper arm, since cameras placed in line with the direction of movement (as opposed to perpendicular) demonstrate poor inter-observer agreement (45), and presumably lower accuracy as well. Although video recording with synchronized cameras at orthogonal angles has been performed in manufacturing contexts (45), it was not practical for full-day recordings of baggage handling work given its dynamic nature, nor would it be appropriate with similar constraints in construction, warehousing, agriculture, or resource industries. Also, it would probably entail an increased cost for collecting and processing data. Furthermore, the effect of changing camera angles from 0 to 90° on the exactness of posture observation has been shown to be small (54), and single cameras are acceptable for determining trunk posture in many cases (45).
The observation method used here employs smaller exposure bins (ie, of 1°) than many other observation methods where bins of 15 or 30° are typically used. This was done to allow for treatment of inclination as a continuous variable, both when obtained from observation and from inclinometers, and thus facilitate direct comparison of observation and inclinometer measurements at the same level of resolution. Data on a continuous scale are also a prerequisite for calculating two of our three exposure variables (ie, the median and the 90th percentile). The cost efficiency of categorical observation, which may be performed faster than the high-resolution observation applied by us, is an interesting issue for additional research.
Comparing different body parts: trunk versus upper arms
In the current study, median trunk and arm inclination are more precisely estimated using observation, while inclinometry is more precise for arm 90th percentile and % time >60° (table 2). The two methods have almost the same precision for trunk 90th percentile and % time >60°. Inclinometry performs better for all arm and trunk posture variables if bias is also taken into consideration. The performance by total study cost is very similar for observation of both body parts when considering combined bias and precision (figure 1b,1d, and 1f). Given the scale of the bias, it seems likely that (especially at larger sample sizes) the measurement performance will be more similar for different body parts using the same method than for the same body part using different methods. That is, once a method is selected it would appear that additional body parts could be assessed with similar performance. Although this appears mostly true for the trunk and the upper arm, these are also two of the largest and easiest-to-assess body segments. Observation error can increase for smaller body parts (45), when the viewing angle is altered (54), and when higher resolution is demanded. Thus, our cost-efficiency results are more likely to be representative for large body parts moving through large ranges of motion, for example hip flexion or knee flexion rather than movement of smaller segments like ulnar deviation or finger flexion.
Considering alternative research scenarios
Scenario 2 acknowledges the savings gained when a research team has the protocols, trained staff, and equipment to immediately
embark on a similar study without the labor of methods development and study planning and the capital cost of equipment. Since
total study cost is lower, the statistical performance (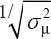 or 1/RMSEμ) obtained at a certain budget is larger in scenario 2 (figure 2) than scenario 1 (figure 1). Performance at a particular sample size does not change in scenario 2 compared to scenario 1, so cost efficiency for both
inclinometry and observation is better in scenario 2 than in scenario 1, while the relationship between the two methods is
maintained.
or 1/RMSEμ) obtained at a certain budget is larger in scenario 2 (figure 2) than scenario 1 (figure 1). Performance at a particular sample size does not change in scenario 2 compared to scenario 1, so cost efficiency for both
inclinometry and observation is better in scenario 2 than in scenario 1, while the relationship between the two methods is
maintained.
It is not unusual for researchers to repurpose previously collected data to answer an additional research question. This might be in the form of resampling existing direct measurements (1, 12, 13), or repeated observation of video film to investigate inter-rater differences or compare different processing schemes (21, 32). Scenario 3 describes a situation where no new data collection is required, resulting in a substantial reduction in total study cost. The reduction in cost is more pronounced for the inclinometer method, since the data processing costs for the chosen observation protocol make up a large proportion of the total cost of that method. Due to this decreased total study cost, inclinometer demonstrates greater performance at a certain budget, when considering either only precision or bias and precision combined. One exception is median trunk angle, where observation performs better in terms of precision than inclinometer for study costs over €30 000 (figure 3a). As with the other two scenarios, inclinometer shows greater advantages in cost efficiency when combined bias and precision are considered.
Choosing a measurement method
In this study, we rank exposure assessment methods on the basis of cost efficiency. However, there are additional qualitative considerations when selecting a measurement method. Although the current study has compared several exposure metrics for postural angles, a comprehensive biomechanical assessment could involve measures of force, muscle activity, manual materials handling, and exposure to contact forces or vibration. Observation has been identified as a more versatile method than direct measurements; if assessment of multiple types of exposure is desired, a single observation protocol might more easily assess several of these aspects (27). Because of this, observation is uniquely suited for screening; checklists and screening instruments can be used to identify potentially harmful situations or particularly exposed body parts worthy of more in-depth analysis using a direct measurement method (47). In contrast, a single inclinometer can deliver only data on postural angle of the body part on which it is mounted and derivatives thereof, such as movement velocities.
The results presented here suggest that, in most scenarios, inclinometry was the more cost-efficient alternative for data collection, which confirms the presumed immutable “exposure assessment hierarchy”. It is not clear, however, whether our specific results can be extrapolated to other techniques for direct measurement and observation and to what extent they apply even to other posture variables. While, for instance, movement frequency, forces applied, and loads in manual handling tasks are difficult to assess at all by observation, several exposure metrics may be more easily observed than monitored by technical equipment; for instance frequency of lifting or nature of manual handling (i.e. push vs. pull vs. lift vs. carry). Thus, precision, bias, and cost efficiency is probably highly specific to the exact method used for exposure assessment.
An additional factor of concern when deciding for measurement instrument(s) in a particular exposure assessment is the possible need to involve highly educated staff when dealing with collection and, especially, processing of directly measured exposures. In the present study, it was not possible to estimate the cost of training the inclinometer processers, as these were the same researchers who developed and tested the inclinometer processing software so the two costs were intertwined. It could be argued that this expertise is accounted for in the hourly wage of skilled researchers, but there may be other situations where researchers do not have specific expertise in the instrumentation at hand and will need to spend specific time training. Where this is the case, the fixed cost of inclinometer would increase, thereby skewing the cost-efficiency results to favor observation. The results of the present study do quantify separate costs for observation software development and training, so the comparison between measurement methods and the extrapolation to other situations should be considered carefully within the local context. It should be noted that as technology and methods develop, skills must be maintained and developed, otherwise one can imagine a “depreciation” of skills and training over time, just as seen with equipment and other capital.
In the future, advancements in technology towards cheaper instruments and trends of more highly automated data processing can have an impact both on the performance of direct measurements and their cost. Technological advancements may also have an impact on video analysis through the use of image pattern recognition, allowing for partial or complete automation and decreased processing costs. The numerical results presented here can be considered a detailed quantification of cost efficiency only as far as technology, equipment, and labor costs remain stable; large changes in these factors would require a recalculation using our methodology with updated cost and performance data as inputs.
Concluding remarks
By the comparison of two different methods for assessing trunk and upper-arm inclination (inclinometry and video-based observation) in terms of their cost efficiency, this study joins an overall limited body of research that quantifies and compares the cost efficiency of exposure assessment methods. The results demonstrate that at a certain total study cost, higher precision estimates of median exposure were delivered using observation, while time spent at angles >60° as well as the 90th percentile arm angle were determined with better precision using inclinometer. When adopting the standard assumption of inclinometers providing correct angular data, observations were shown to be biased. Adding this bias into the metric for statistical performance led to inclinometers consistently outperforming observations for all posture variables, irrespective of scenario.
While this study has been devoted mainly to assessment of working postures, we propose that assessment of cost efficiency is an important step in informed epidemiologic study design in general. To that end, we recommend our approach of calculating costs using a comprehensive cost model, assessing statistical performance on the basis of exposure variance components and suspected bias, and then merging the two in a quantitative relationship between cost and performance.